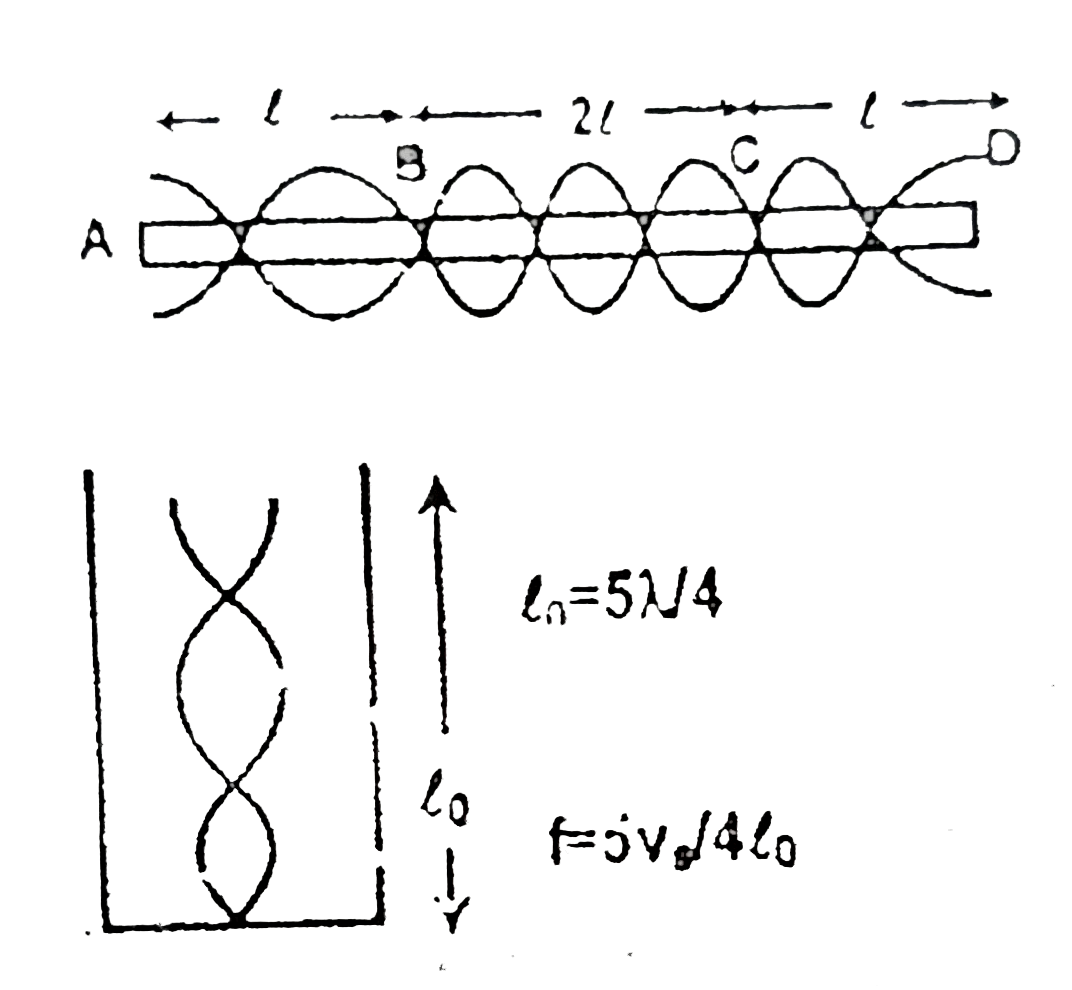Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
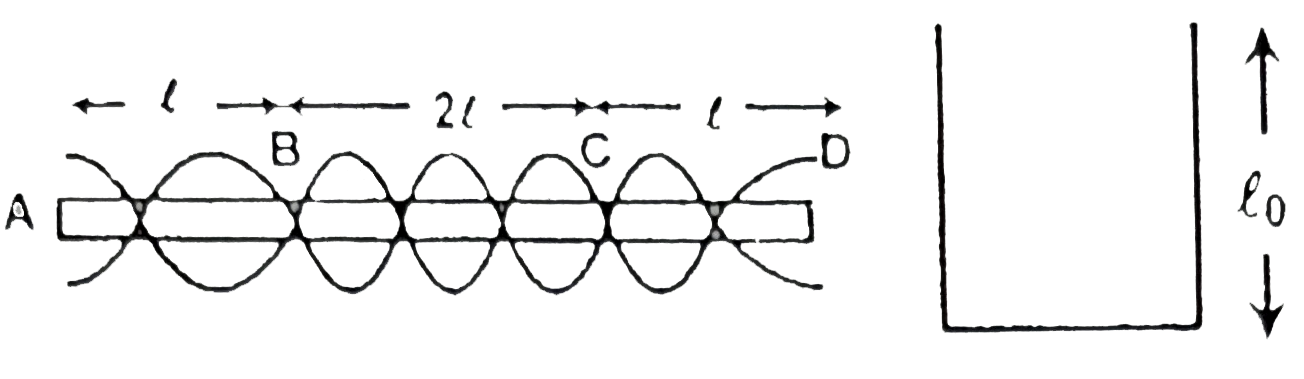
- A closed orgain pipe of length l(0) is resonating in 5^(th) harmonic m...
Text Solution
|
- An aluminium rod having a length of 90.0 cm is clamped at its middle p...
Text Solution
|
- A rod of nickel of length l is clamped at its midpoint . The rod is st...
Text Solution
|
- Consider a rod of length l resting on a wall and the floor. If the vel...
Text Solution
|
- A steel rod of length 100 cm is clamped at the middle. The frequency o...
Text Solution
|
- A uniform rod of mass m and length l is rotating with constant angular...
Text Solution
|
- एक पतली छड़ का द्रव्यमान M तथा लम्बाई l है। छड़ के एक सिरे से l//3 दूरी ...
Text Solution
|
- एक छड़ के पदार्थ का घनत्व rho=A+Bx के अनुसार बदलता है , जहाँ A,B अचर है...
Text Solution
|
- A uniform rod of length L is rotated in a horizontal plane about a ver...
Text Solution
|