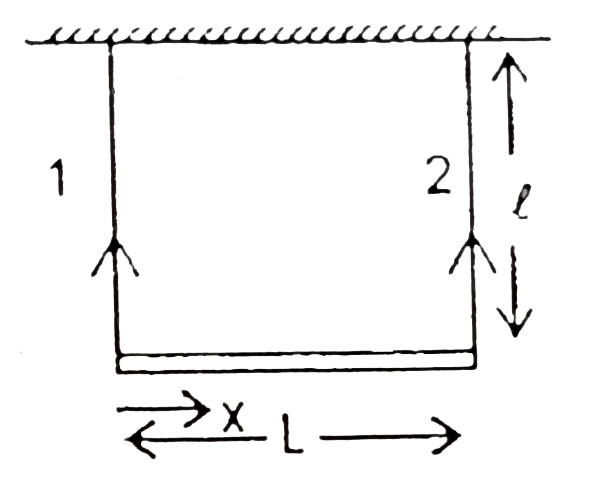
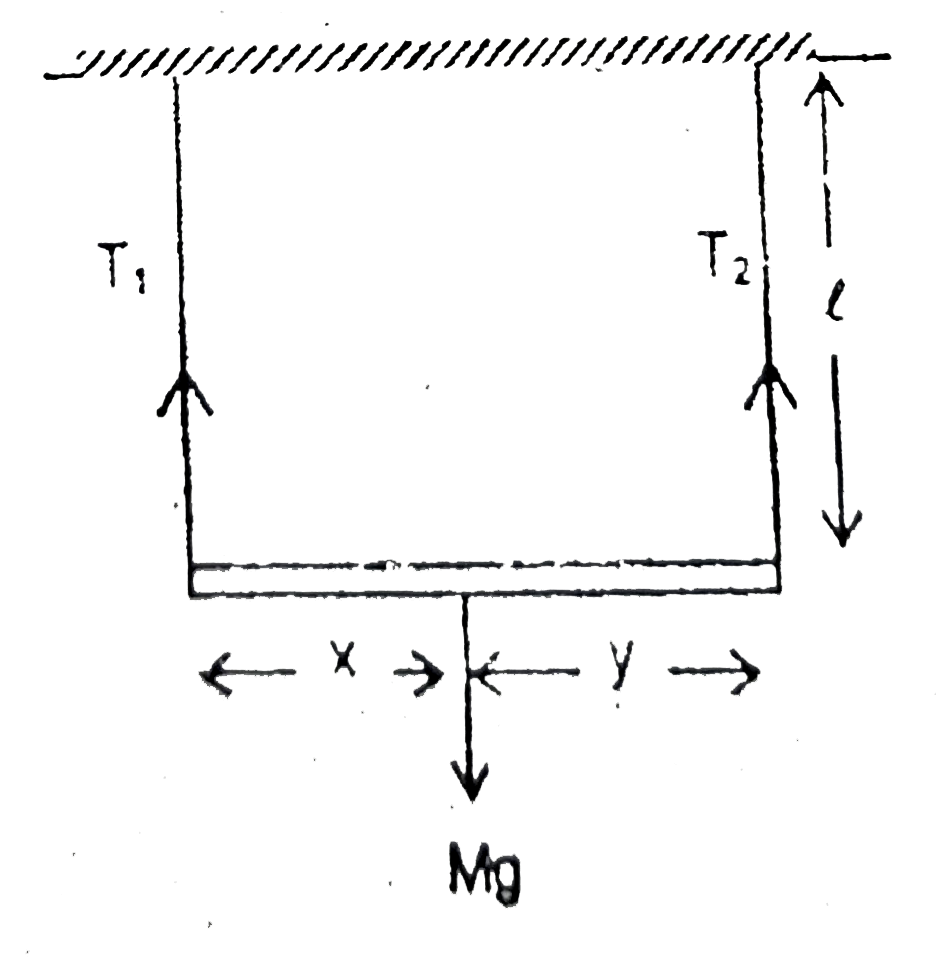
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two strings of the same length but different mass per unit length are ...
Text Solution
|
- A string of mass per unit length mu is clamped at both ends such that ...
Text Solution
|
- String-1 is connected with string-2 The mass per unit length in string...
Text Solution
|
- The frequency 'n' of a stretched string depends on length 'l' of a str...
Text Solution
|
- A string of length and mass per unit length is used in atwood mach...
Text Solution
|
- The frequency of vibration of a string depends of on, (i) tension in t...
Text Solution
|
- A string of mass per unit length "0.2 kg m"^(-1) and length 0.6 m is f...
Text Solution
|
- A transverse wave is propagating on a stretched string of mass per uni...
Text Solution
|
- The frequency ( nu ) of transverse wave on a string may depend upon (i...
Text Solution
|