Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
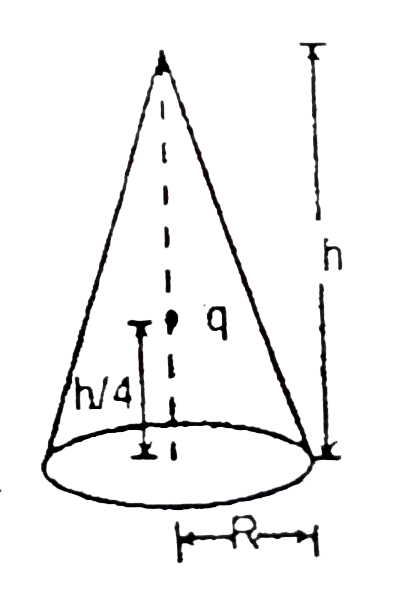
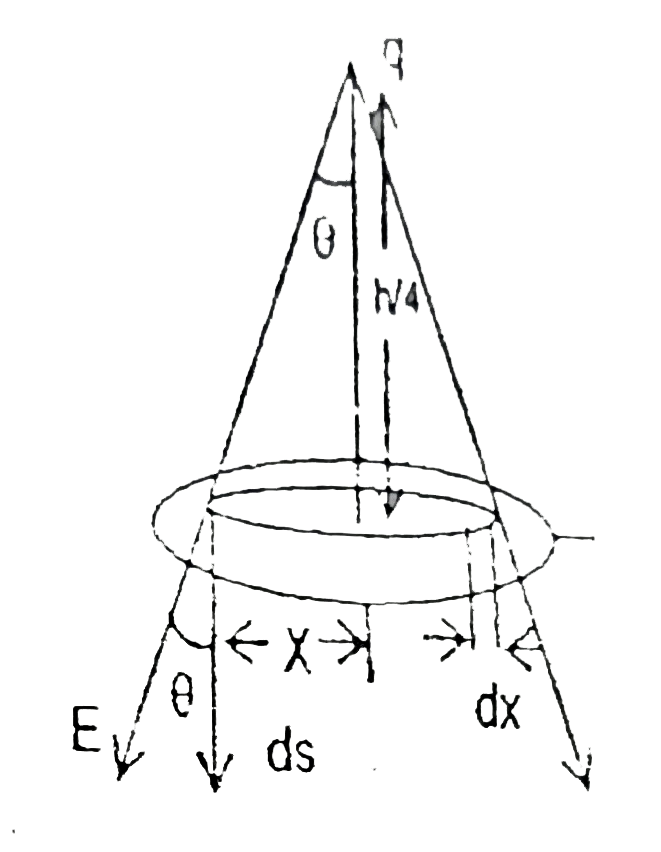
- A charge q is placed at a height (h)/(4) from the base of a cone of he...
Text Solution
|
- A conic surface is placed in a uniform electric field E as shown in fi...
Text Solution
|
- Find the CG of :(a) a cone of height h from the base,(b) a hemisphere ...
Text Solution
|
- The radius of base of a cone is r and height is h. Find its volume.
Text Solution
|
- The curved surface area of a right circular cone of height h unit and...
Text Solution
|
- एक शंकु के आधार की त्रिज्या r और ऊँचाई h है। इसका आयतन ज्ञात कीजिए।
Text Solution
|
- The curved surface area of a cone of base radius r and height h is.
Text Solution
|
- From a uniform solid cone of base radius R and height H, a symmetric c...
Text Solution
|
- Curved surface area of cone of height H and radius R is
Text Solution
|