Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
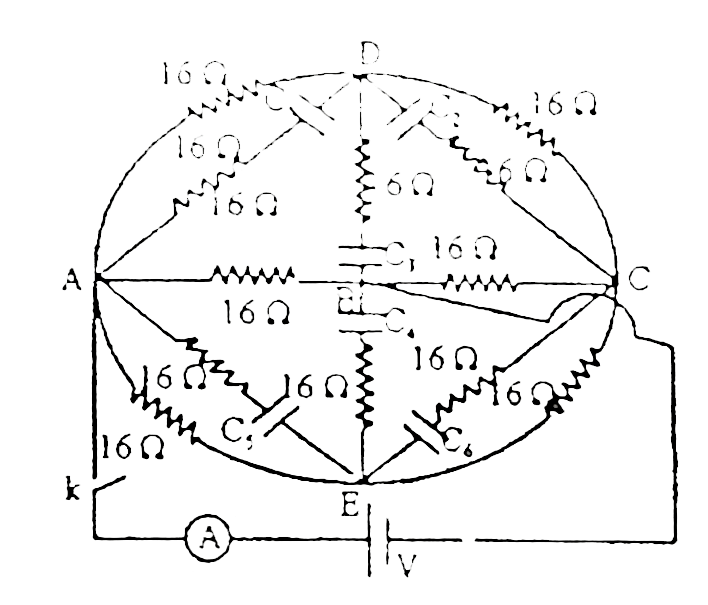
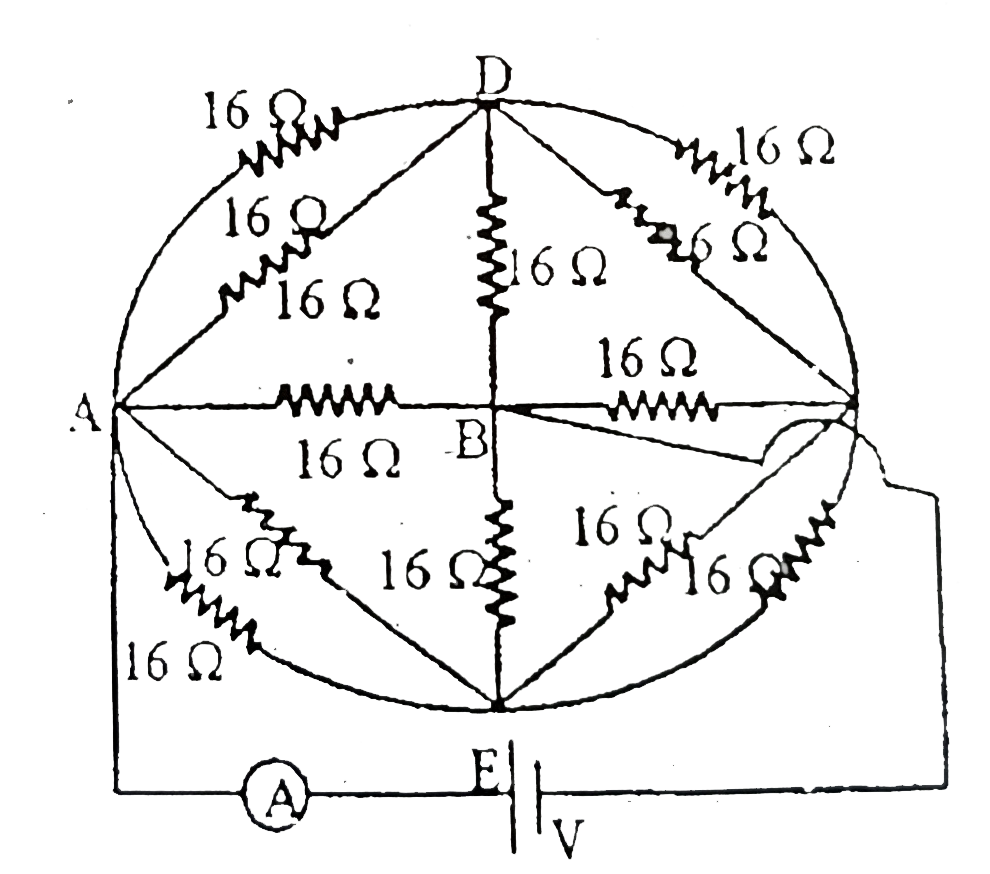
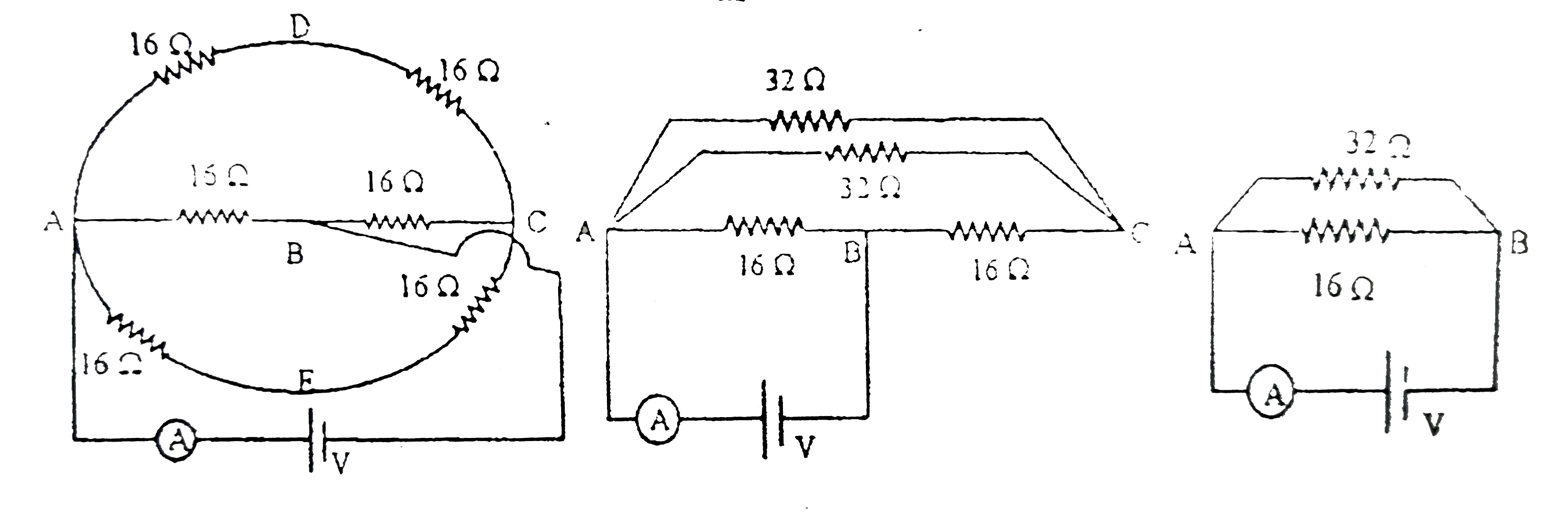
- The resistance each of 16 Omega and capacitance of each 100 mu F are a...
Text Solution
|
- A 20(mu)Fcapacitor is joined to a battery of emf 6.0V through a resist...
Text Solution
|
- A capacitor of capacitance 100(mu)F is connected across a battery of e...
Text Solution
|
- For the circuit arrangement shown in fig. a. Find the potentail d...
Text Solution
|
- Four capacitor and a battery of emf 24 V are connected as shown in the...
Text Solution
|
- n resistances each of resistance R are joined with capacitors of ca...
Text Solution
|
- In the circuit shown, r = 4 Omega, C = 2mu F (a) Find the current comi...
Text Solution
|
- Three identical charged capacitors each of capacitance 5 mu F are conn...
Text Solution
|
- A network of four capacitors, each of capacitance 15muF,is connected a...
Text Solution
|