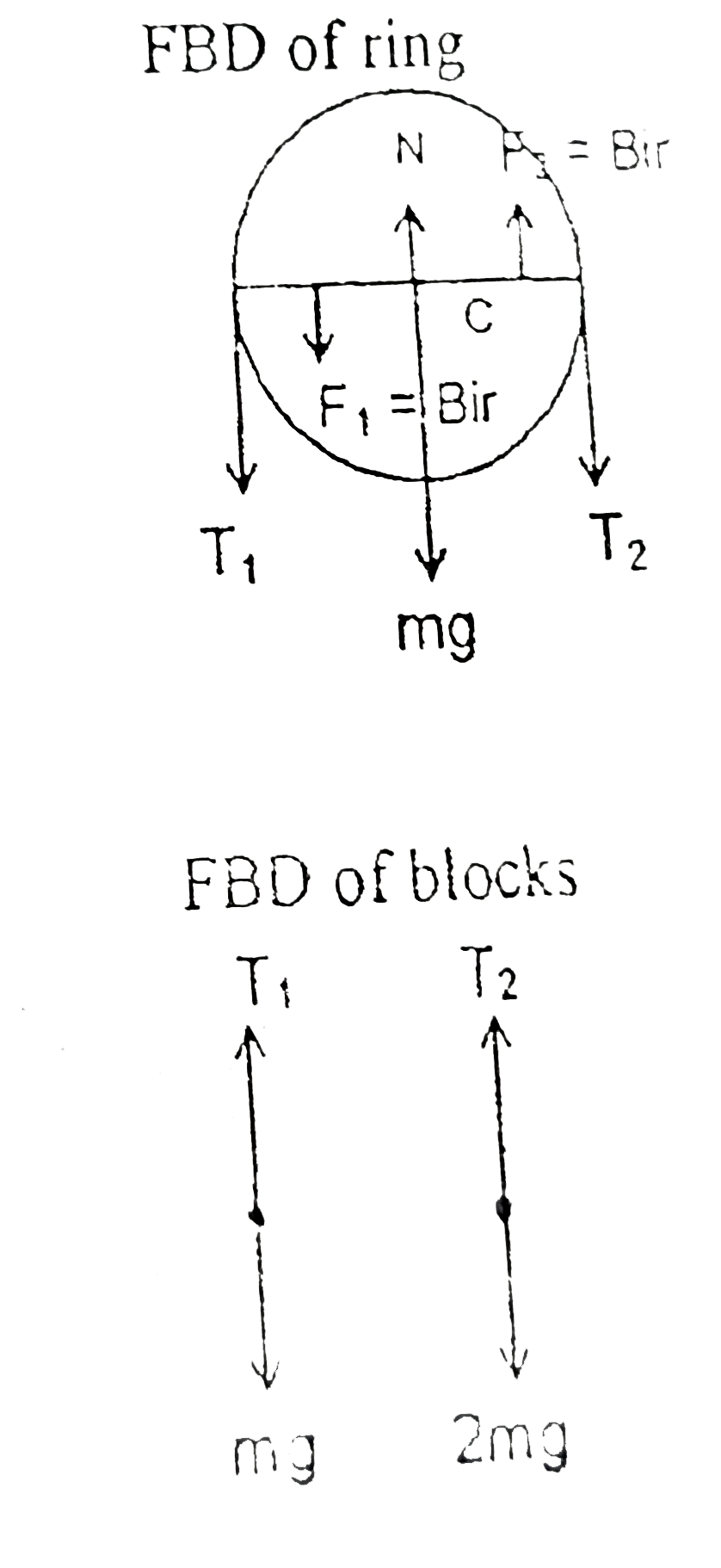Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A conducting ring of mass m and radius r has a weightless conducting r...
Text Solution
|
- A conducting ring of mass m and radius r has a weightless conducting r...
Text Solution
|
- A conducting ring of mass m and radius r has a weightless conducting r...
Text Solution
|
- Solve problem 15 if the length of rod is 2L and resistance 2r and it i...
Text Solution
|
- A disc of mass M = 2m and radius R is pivoted at its centre. The disc ...
Text Solution
|
- There is a ring or mass m and radius R is pivoted at a point O on its ...
Text Solution
|
- A ring of mass M and radius R is at rest at the top of an incline as s...
Text Solution
|
- A disc of mass m and radius r is free to rotate about its centre as sh...
Text Solution
|
- A ring of mass m and radius R is rolling on a horizontal plane. If the...
Text Solution
|