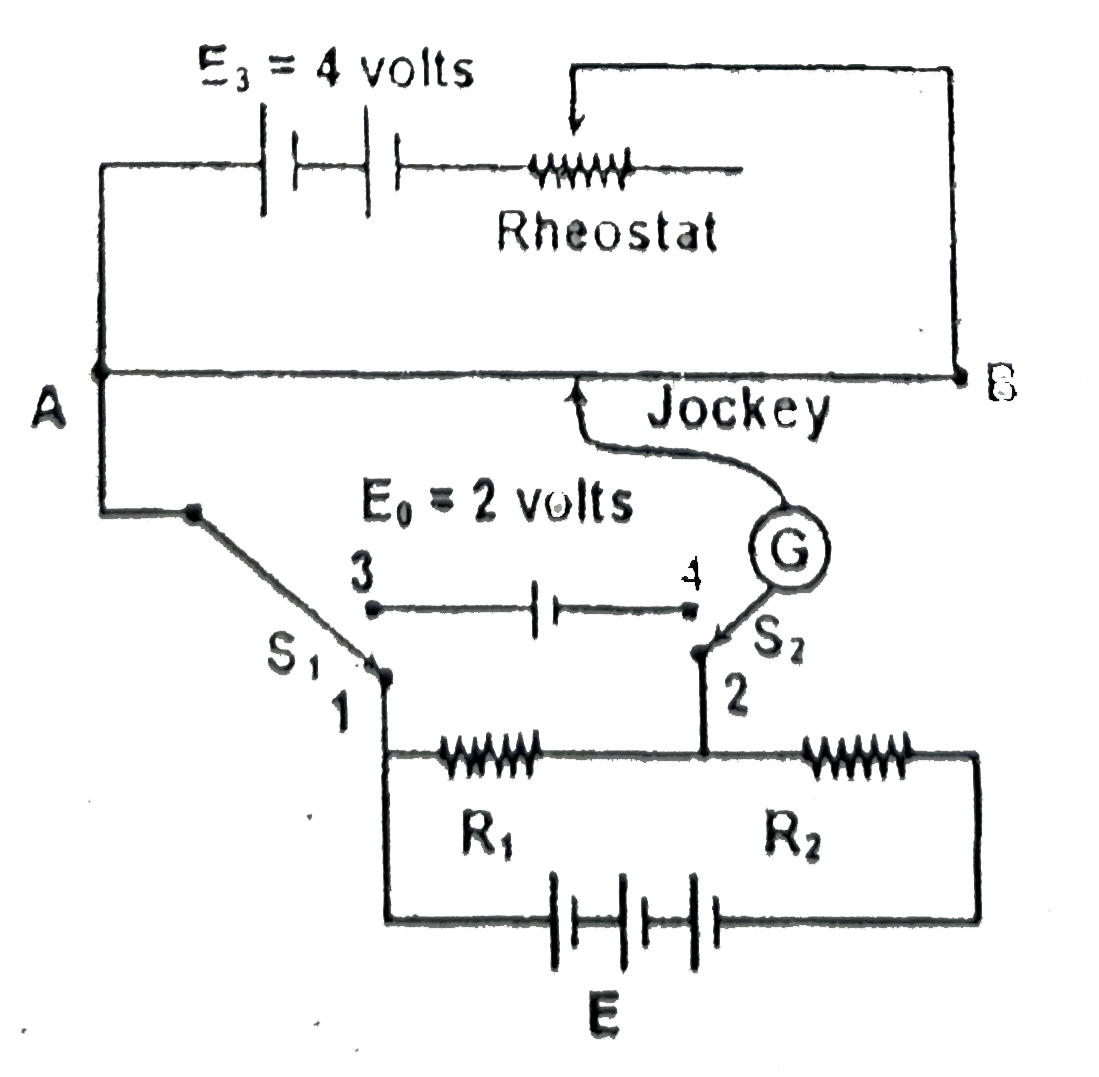
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the labortary, the high emf of a battery is measured by using poten...
Text Solution
|
- The resistance in the left and right gaps of a balanced meter bridge a...
Text Solution
|
- The figure represents two concentric shells of radii R(1) and R(2) and...
Text Solution
|
- The figure shown gives values of R(1 ) and R(2), the balance point for...
Text Solution
|
- Two resistance R(1) and R(2) when connected in series and parallel wit...
Text Solution
|
- A capacitor C is connected to a battery circuit having two switches S(...
Text Solution
|
- In the circuit shown in the figure R(1) = R(2) = 5 Omega, C(1) = C(2) ...
Text Solution
|
- The resistors R(1),R(2),R(3) and R(4) are connected as shown in the fi...
Text Solution
|
- Statement I In a Delta ABC, if a lt b lt c and ri si inradius and r(1)...
Text Solution
|