Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
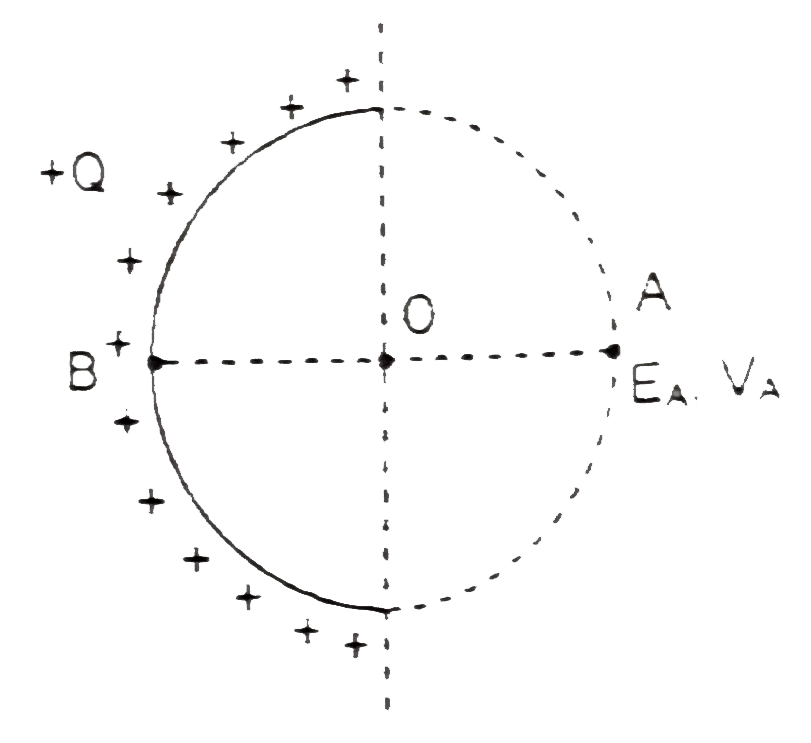
- A non-conducting wire is bent into a semi-circle of radius R and a cha...
Text Solution
|
- Find the potential difference V(a)-V(b)in the circutis shown in figure
Text Solution
|
- In the circuit as shown, V(A) - V(B) = V. The resistance of each wire ...
Text Solution
|
- A charge Q is distributed uniformly on a ring of radius R as shown in ...
Text Solution
|
- A charge Q is uniformly distributed inside a non- conducting sphere of...
Text Solution
|
- A non-conducting semi circular disc (as shown in figure) has a uniform...
Text Solution
|
- In the circuit shown in figure 3.154 find the potential difference V(A...
Text Solution
|
- A charge Q is distributed uniformly on a ring of radius R as shown in ...
Text Solution
|
- In the figure shown, conducting shells A and B have charges Q and 2Q d...
Text Solution
|