Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
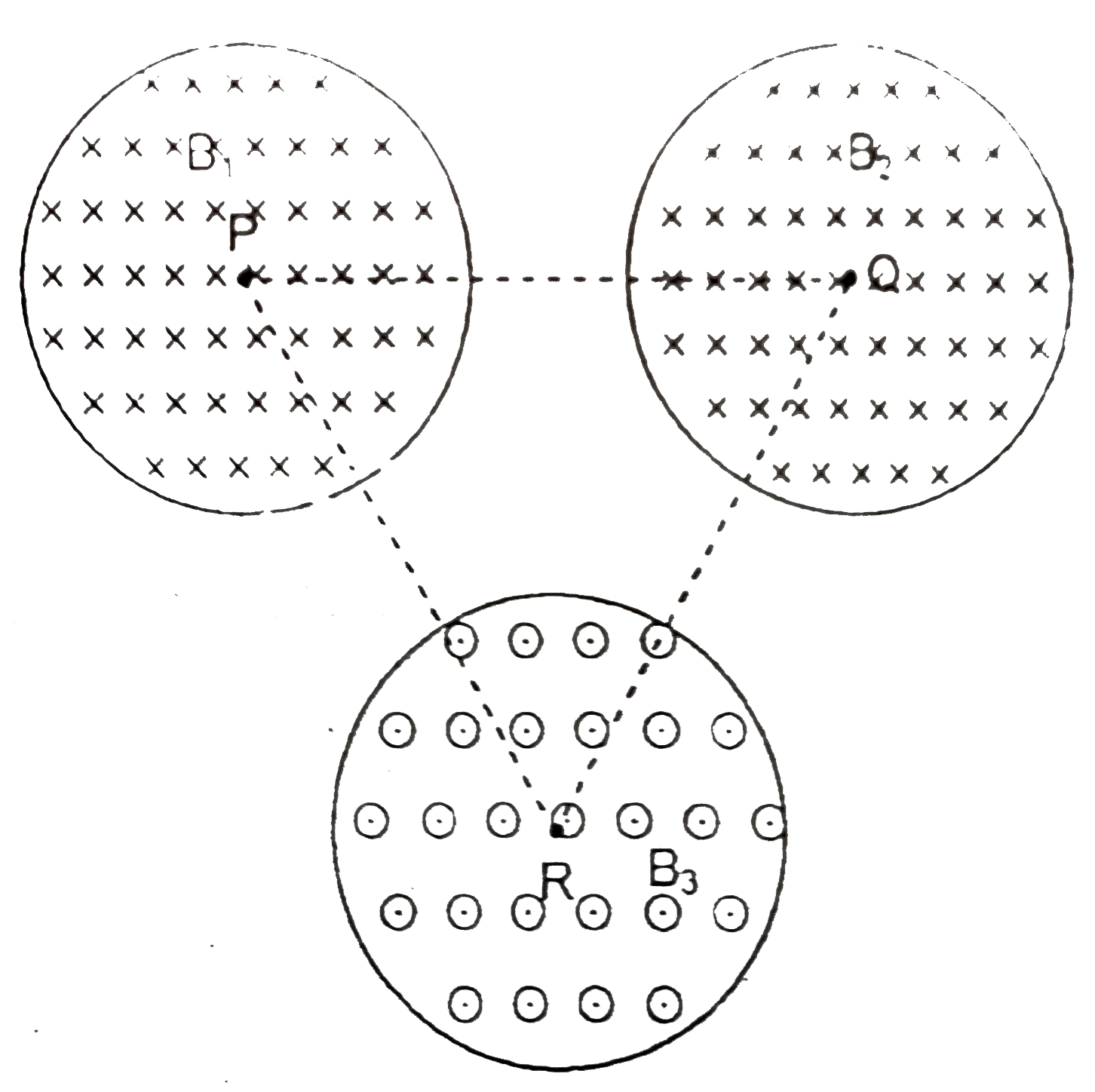
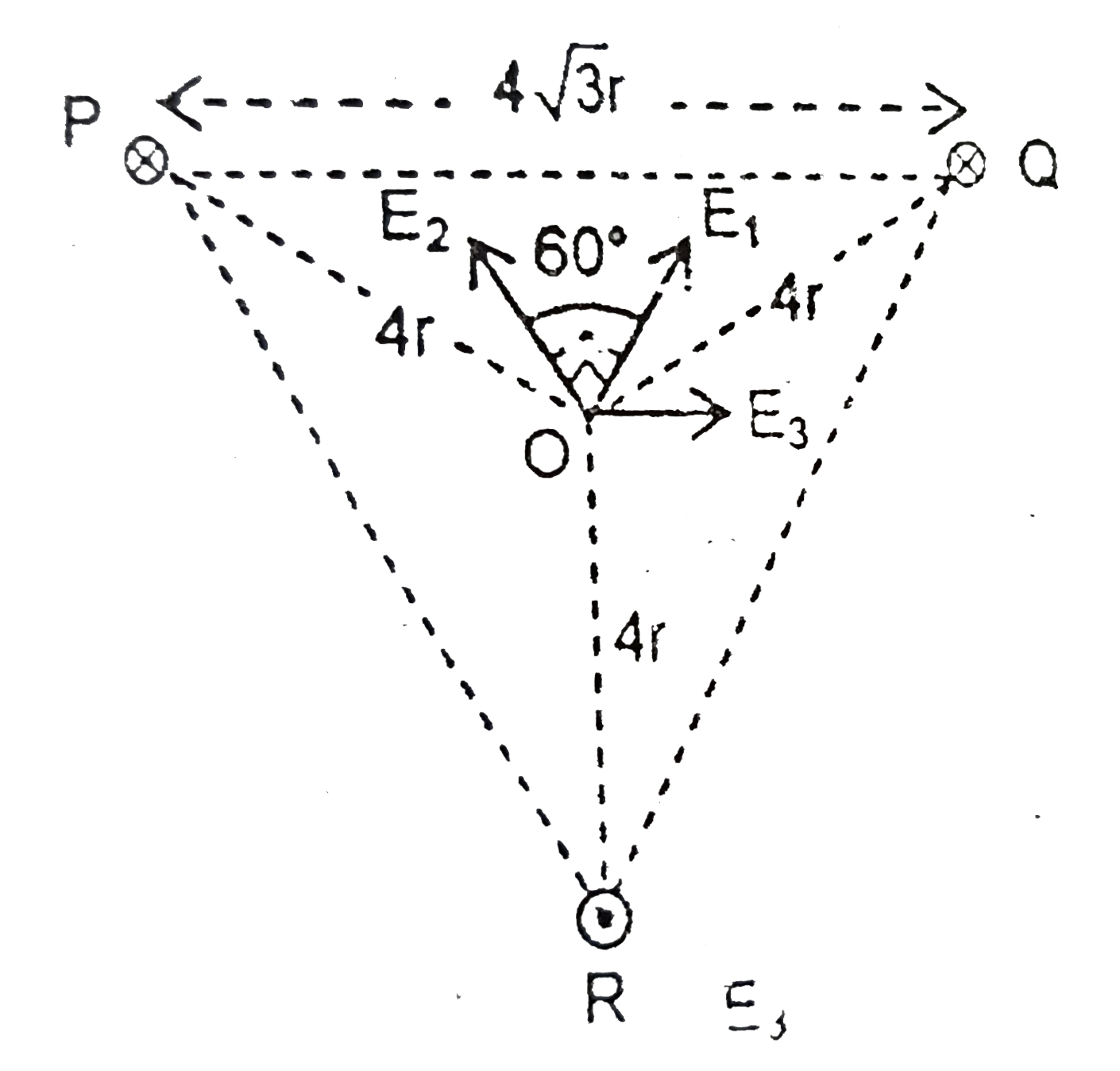
- In the figure B(1), B(2) and B(3) represent uniform time varying magne...
Text Solution
|
- A time varying magnetic field is present in a cyclindrical region R as...
Text Solution
|
- An infinitely long cylinderical wire of radius R is carrying a current...
Text Solution
|
- Five balls b(1),b(2),b(3),b(4),b(5) are kept at random in five foxes B...
Text Solution
|
- A uniform magnetic field exists in the space B=B(1)hati+B(2)hatj-B(3)h...
Text Solution
|
- Let S be the set of all column matrices [(b(1)),(b(2)),(b(3))] such th...
Text Solution
|
- If b(1),b(2),b(3),"….."b(n) are positive then the least value of (b(1)...
Text Solution
|
- Let S be the set of all column matrices [(b(1)), (b(2)), (b(3))] such ...
Text Solution
|
- Statement -1 Consider the determinant Delta=|{:(a(1)+b(1)x^(2),a(1)x...
Text Solution
|