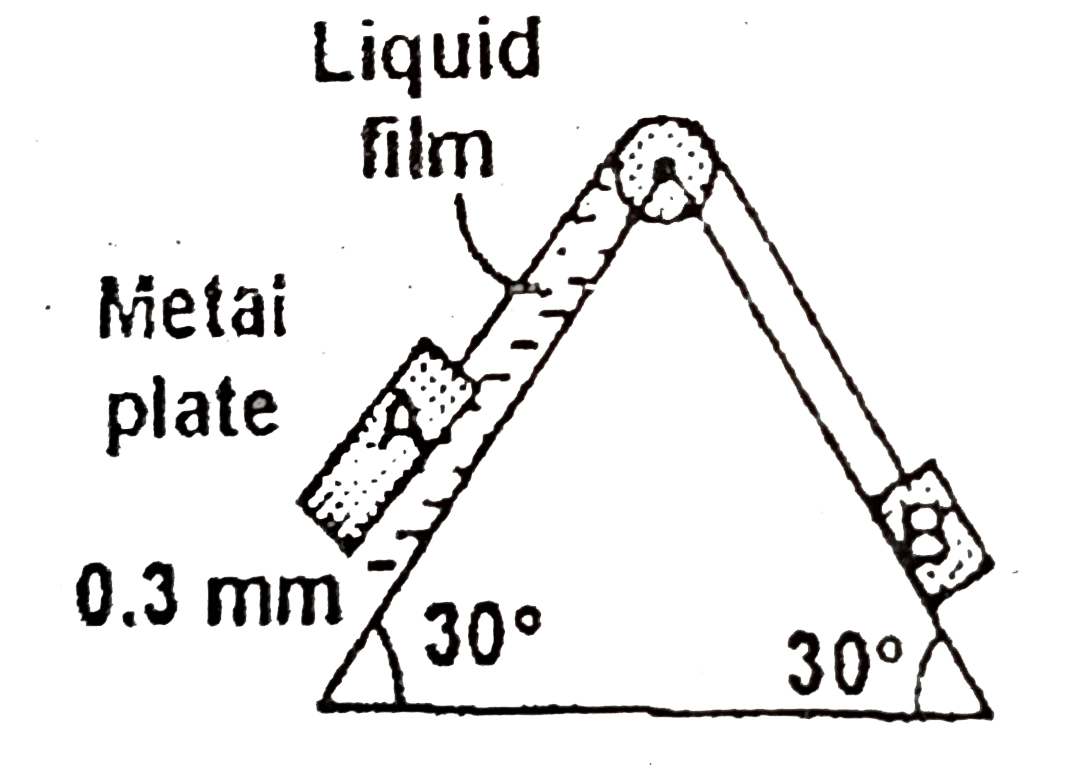
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A metal plate of area 0.10 m^(2) is connected to a 0.04 kg mass via a ...
Text Solution
|
- A metal plate of area 0.10m^(2) is connected to a 0.01 kg mass via a s...
Text Solution
|
- A metal block of area 0.10 m^(2) is connected to a 0.01 kg mass via a ...
Text Solution
|
- 0.10 m^(2) क्षेत्रफल की कोई धातु की प्लेट किसी डोरी की सहायता से जो एक...
Text Solution
|
- A metal block of area 0.10 m^(2) is connected to a 0.02 kg mass via a ...
Text Solution
|
- A metal block of area 0.10 m^(2) placed at a table, is connected to a ...
Text Solution
|
- 0.10 " मी"^(2) क्षेत्रफल की एक धातु की प्लेट किसी डोरी सहायता से जो ए...
Text Solution
|
- A metal plate of area 0.10 m^(2) is connected to a 0.01 kg mass via a ...
Text Solution
|
- A metal plate of area 0.10 m^(2) is connected to a 0.01 kg mass via a ...
Text Solution
|