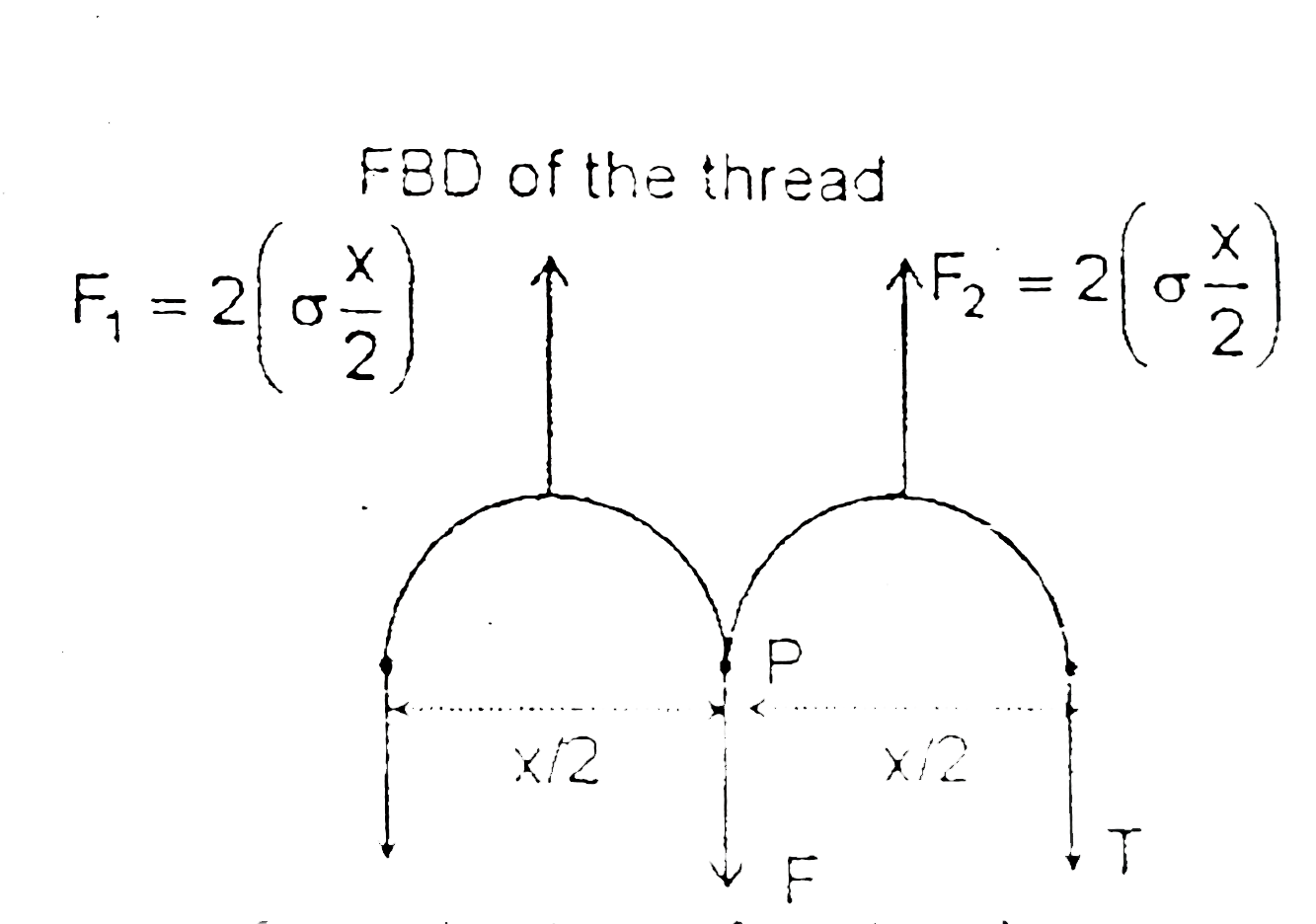A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A thin and light thread of sufficient length L is attached to a wire f...
Text Solution
|
- A wire forming a loop is dipped into soap solution and taken out so th...
Text Solution
|
- A thread is tied slightly loose to a wire frame as in figure and the f...
Text Solution
|
- The figure shows a soap film in which a closed elastic thread is lying...
Text Solution
|
- A film of soap solution is formed on a loop frame loop of 6.28 cm long...
Text Solution
|
- तार से बने एक फ्रेम को साबुन के घोल में डुबोकर बाहर निकाल लिया जाता है...
Text Solution
|
- A thread is tied slightly loose to a wire frame as in figure and the f...
Text Solution
|
- एक धागे को तार के एक फ्रेम पर चित्रानुसार थोड़ा ढीला बाँधा जाता है तथ...
Text Solution
|
- A wire forming a loop is dipped into soap solution and taken out so th...
Text Solution
|