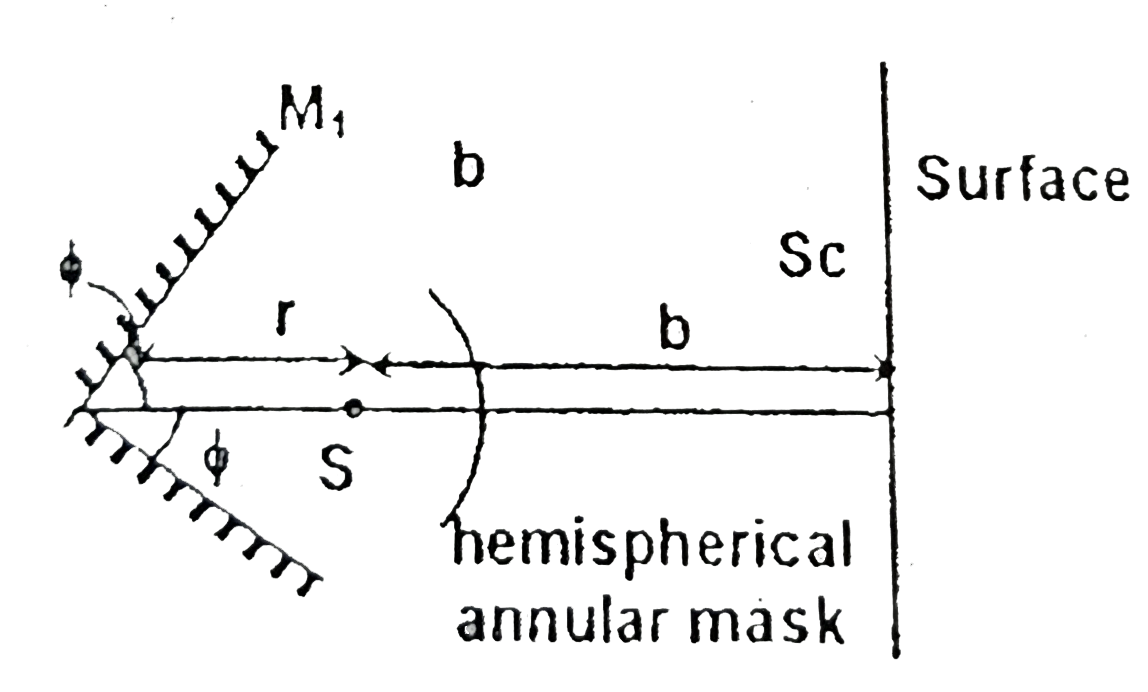
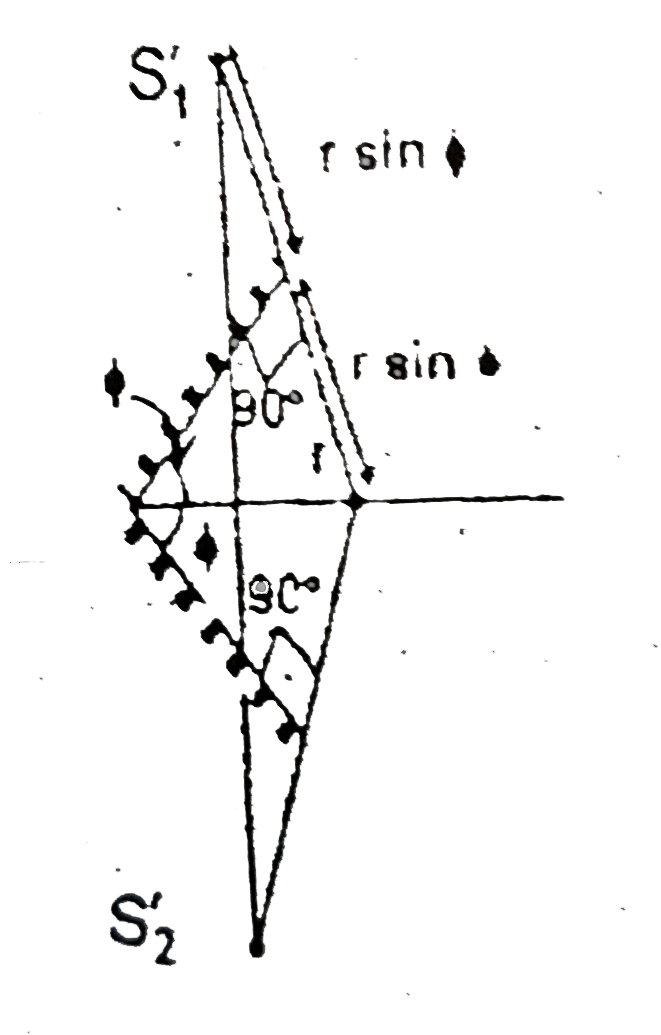
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two mirror M(1) and M(2) make an angle phi with line AB. A point sourc...
Text Solution
|
- M(1) and M(2) are plane mirrors and kept parallel to each other. At po...
Text Solution
|
- A ray of light is incident at an angle of 30^(@) on a plane mirror M(1...
Text Solution
|
- In the figure shown M(1) and M(2) are two spherical mirrors of focal l...
Text Solution
|
- Two plane mirror M(1) "and" M(2) are inclined to each other at 70^(@)....
Text Solution
|
- In the shown figure M(1) and M(2) are two concave mirrors of the same ...
Text Solution
|
- एक अवतल दर्पण M(1) एक बिंदुस्रोत S तथा उत्तर दर्पण M(2) चित्र 34. E4 क...
Text Solution
|
- The mirrors are perpendicular to each other as shown in the Fig. A lig...
Text Solution
|
- Figure shows a point object placed between two parallel mirrors. Its d...
Text Solution
|