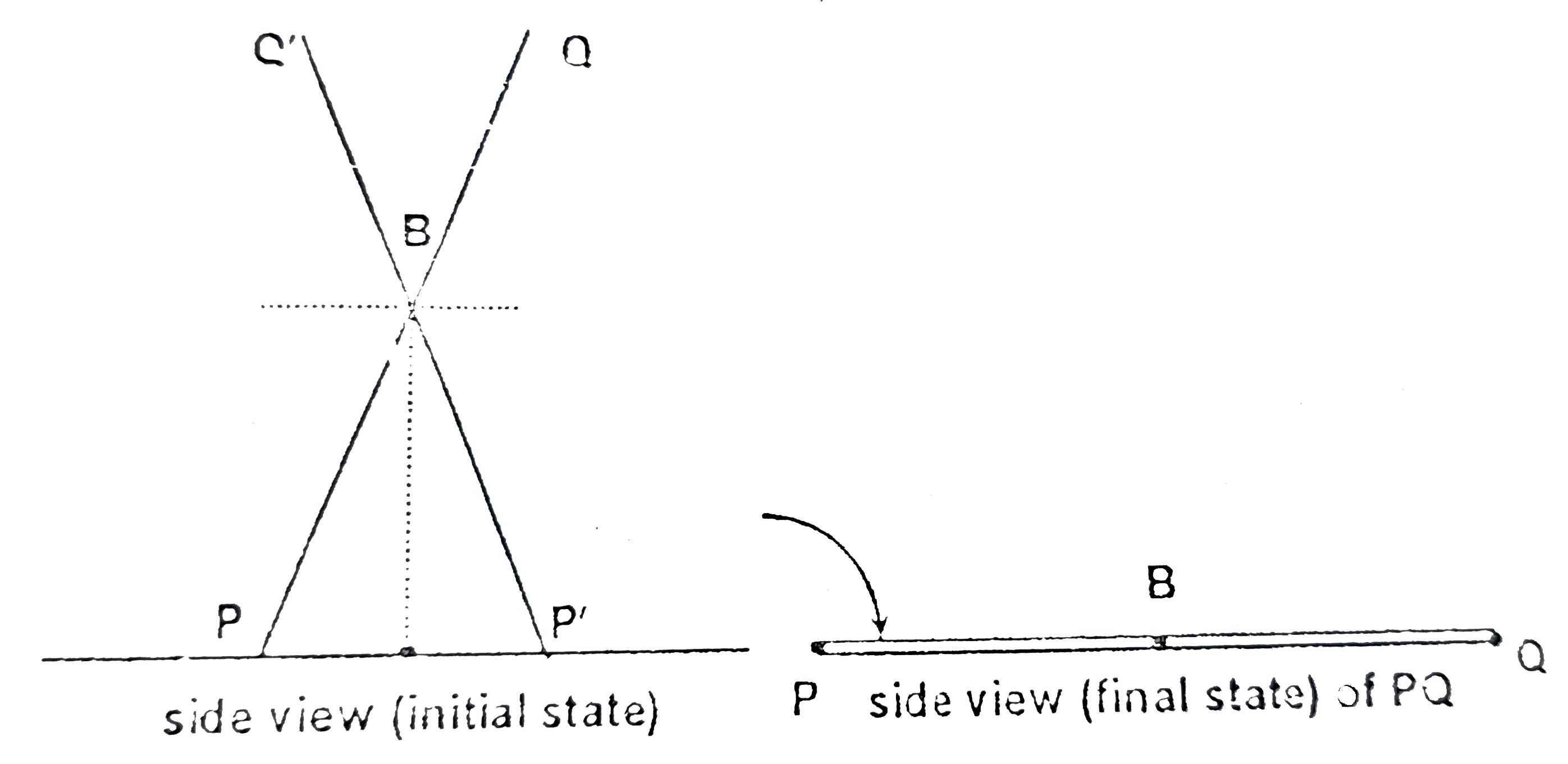A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The two indentical rectangular stell frames with the dimensions shown ...
Text Solution
|
- ABC is an equilateral triangular frame of mass m and side r. It is at ...
Text Solution
|
- (a) there is a rectangular frame of wir measuring 20 cm xx 13 cm . Cal...
Text Solution
|
- Calculate the mutual inductance of a long straight wire and a rectangu...
Text Solution
|
- A conducting square frame of side 'a' and a long straight wire carryin...
Text Solution
|
- A triangular frame consists of three identical rods, each of mass m an...
Text Solution
|
- A uniform rectangular block of dimensions shown in fig is sliding on t...
Text Solution
|
- An L shaped frame is free to rotate in a vertical plane about a horizo...
Text Solution
|
- An L shaped frame is free to rotate in a vertical plane about a horizo...
Text Solution
|