A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
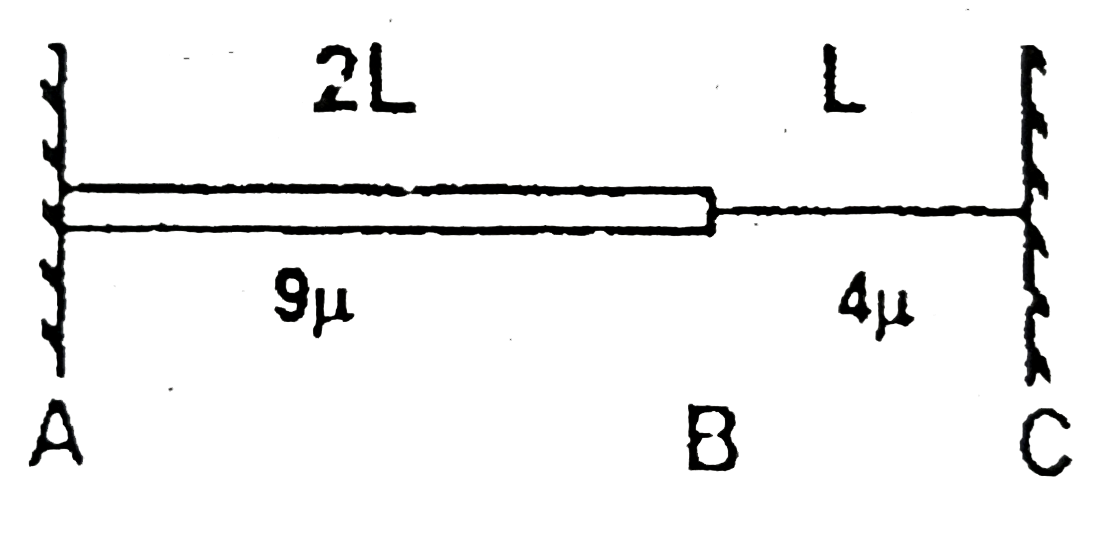
- A thick rope of length 2L and linear mass density 9mu is joined at B t...
Text Solution
|
- A thick rope of density rho and length L is hung from a rigid support....
Text Solution
|
- A uniform rope of length 'L and linear density 'mu' is on a smooth hor...
Text Solution
|
- A body of mass 50 kg is pulled by a rope of length 8 m on a surface by...
Text Solution
|
- A uniform rope of linear mass density lambda (kg/m) passes over a smoo...
Text Solution
|
- STATEMENT-1: A block is pulled along a horizontal frictionless surface...
Text Solution
|
- A loop of rope is whirled at a high angular velocity omega , so that i...
Text Solution
|
- l One end of a thick rope of length is hung from a firm support The de...
Text Solution
|
- A thick rope of density p and length L is hung from a rigid support. T...
Text Solution
|