A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
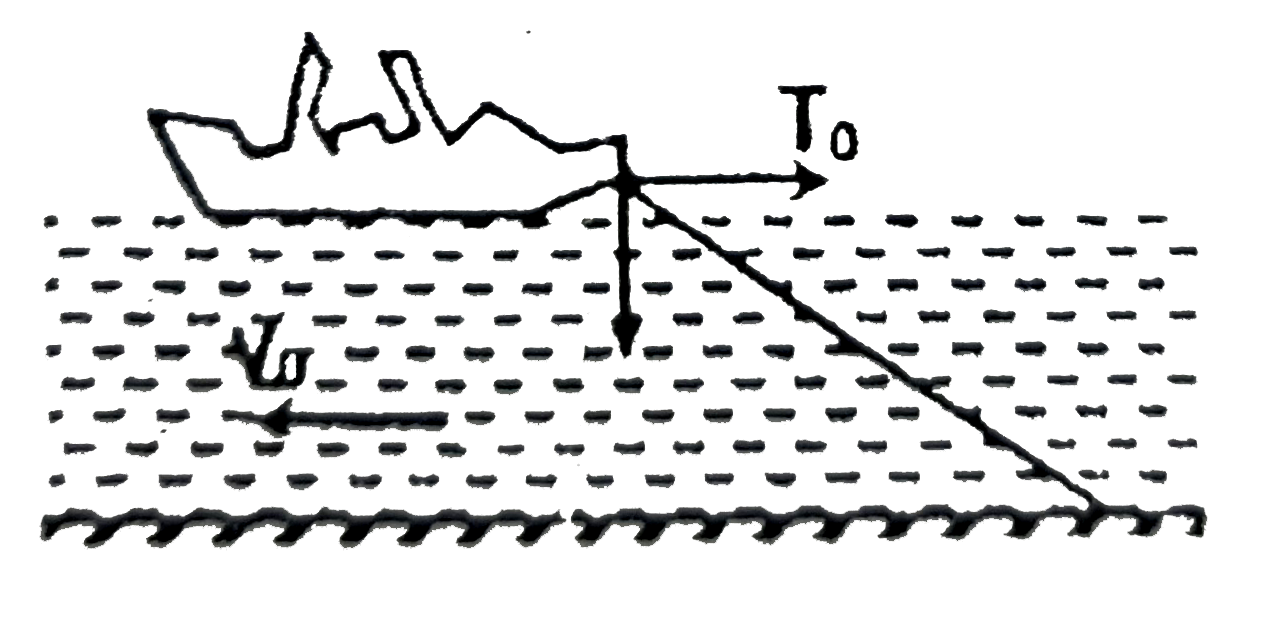
- A ship of total mass m is anchored in the middle of a river and water ...
Text Solution
|
- Ship A moving with velocity vec(V(1)) = 30 hat(i) + 50 hat(j) from pos...
Text Solution
|
- A ship of mass 3xx10^7kg initially at rest, is pulled by a force of 5x...
Text Solution
|
- Two ropes are puling a large ship at rest of mass 1xx106kg into harbou...
Text Solution
|
- A women on the deck of a ship anchored in the ocean observes that the ...
Text Solution
|
- The resistance R to the motion of a ship depends on the velocity v of ...
Text Solution
|
- क्या कारण है कि वायु में जहाज का वेग, जल में जहाज के वेग की अपेक्षा बह...
Text Solution
|
- Figure shows two ships moving in x-y plane with velocity V(A) " and "...
Text Solution
|
- The volume and mass of a buoy are 1000 L and 950 kg respectively. It i...
Text Solution
|