A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
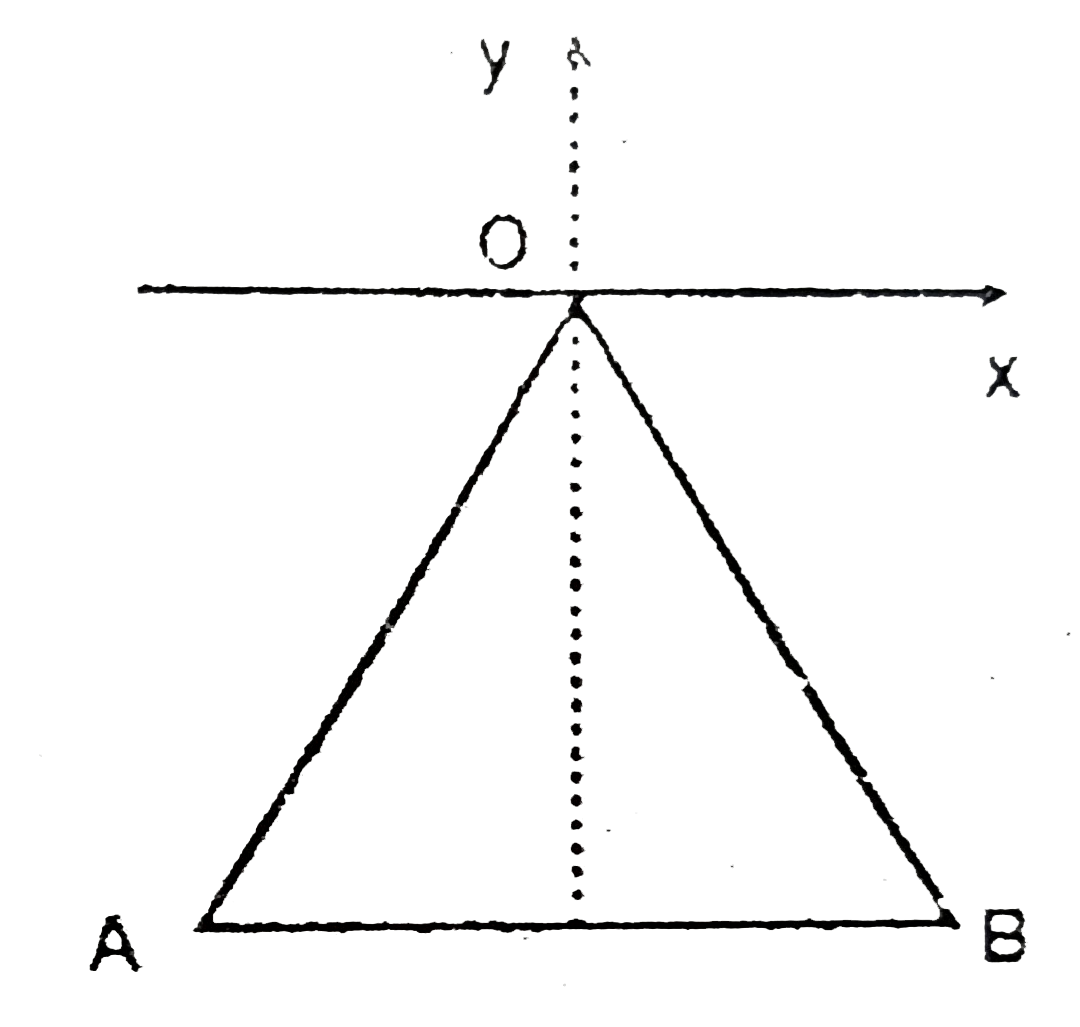
- A triangular of rigid wire frame 'AOB' is made, in which length of eac...
Text Solution
|
- A particle performs SHM on x- axis with amplitude A and rtime period p...
Text Solution
|
- A square plate of mass M and side length L is hinged at one of its ver...
Text Solution
|
- Two identical positive charges Q each are placed on the x axis at poin...
Text Solution
|
- A particle performing SHM takes time equal to T (time period of SHM) i...
Text Solution
|
- A solid cylinder of mass m length L and radius R is suspended by means...
Text Solution
|
- A body performing SHM about its mean position with period 24 s, after ...
Text Solution
|
- A sphere is made to oscillate about a horizontal tangential axis. Dete...
Text Solution
|
- A disc is made to oscillate about a horizontal axis passing through mi...
Text Solution
|