A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
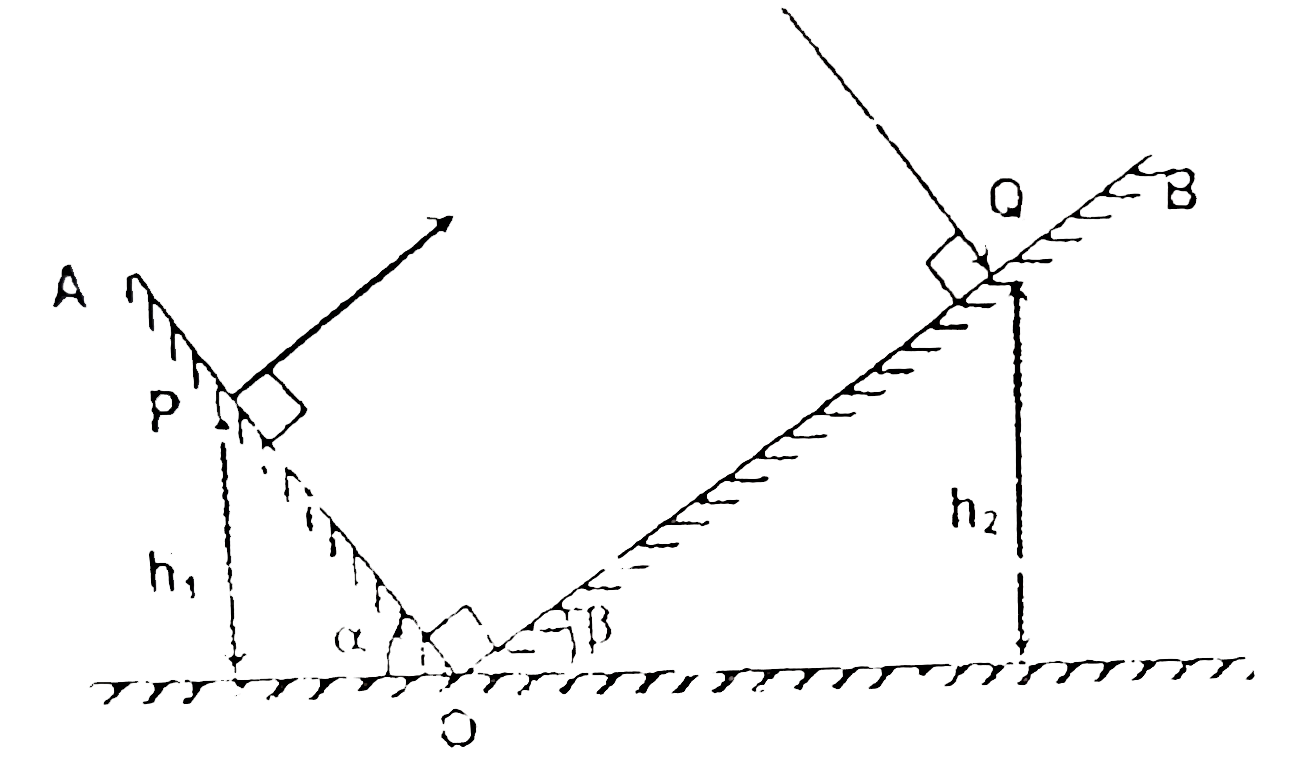
- A particle is projected from point P on inclined plane OA perpendicula...
Text Solution
|
- Two inclined planes OA and OB having inclinations 30^@ and 60^@ with t...
Text Solution
|
- Figure shows that particle A is projected from point P with velocity u...
Text Solution
|
- Two inclined planes OA and OB having inclination (with horizontal) 30^...
Text Solution
|
- Two inclined planes OA and OB having inclination (with horizontal) 30^...
Text Solution
|
- Two inclined planes OA and OB of inclinations alpha and beta equal to ...
Text Solution
|
- Two inclined planes OA and OB intersect in a horizontal plane having t...
Text Solution
|
- Two inclined planes OA and OB intersect in a horizontal plane having t...
Text Solution
|
- Two inclined planes OA and OB intersect in a horizontal plane having t...
Text Solution
|