A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Three point masses m, 2m and m, connected with ideal spring (of spring...
Text Solution
|
- A block of mass m is connect to another block of mass M by a massless ...
Text Solution
|
- A block of mass m is connected to another block of mass M by a spring ...
Text Solution
|
- A block of mass m is connected to another block of mass M by a massles...
Text Solution
|
- Two blocks of masses m and M connected by a spring are placed on frict...
Text Solution
|
- A block of mass m is connected to another .block of mass M by a massle...
Text Solution
|
- Two blocks of mass m and 2m are kept on a smooth horizontal surface. T...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|

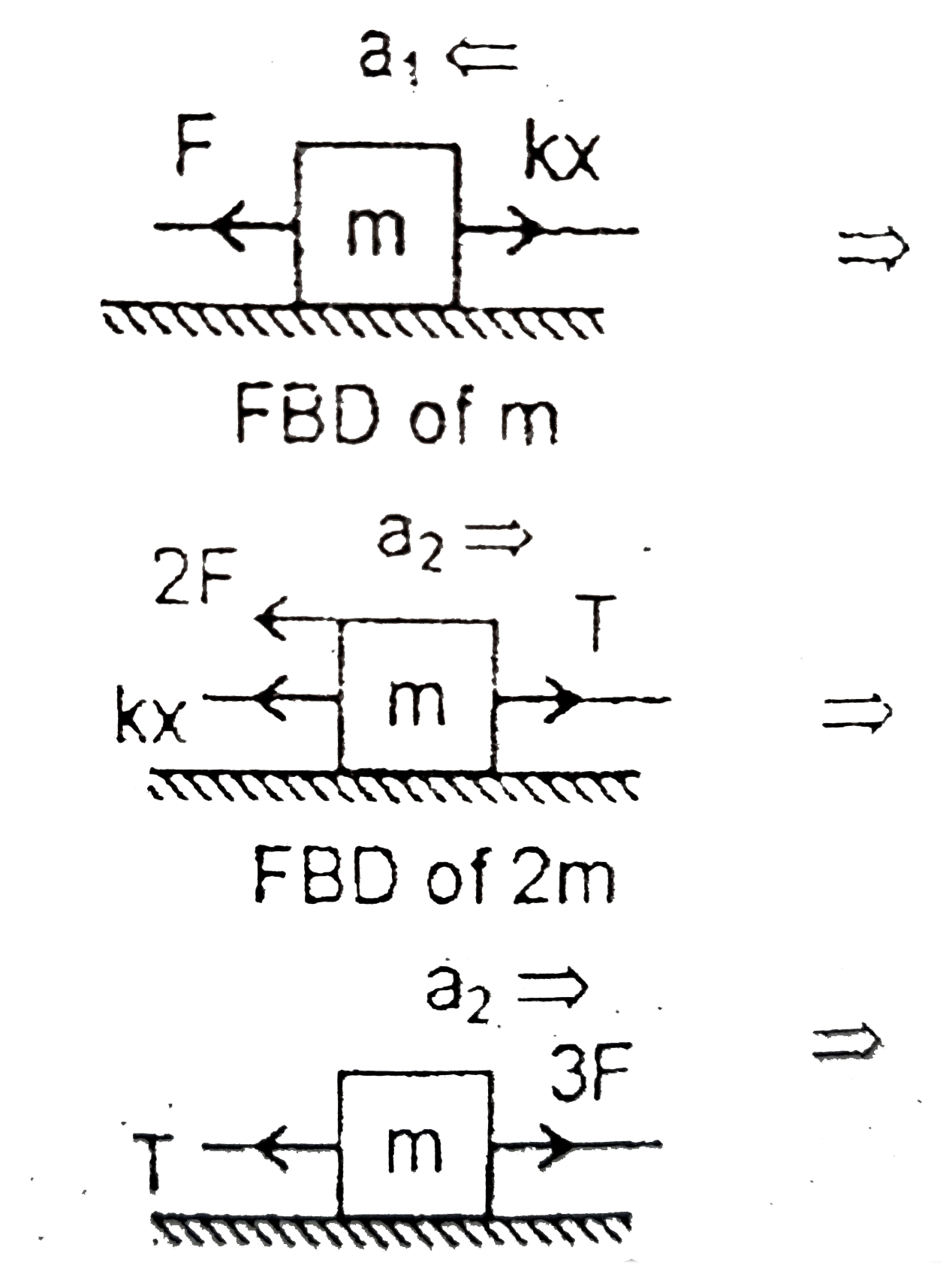 `rArr F-kx=ma_(1)rArr a_(1)=(F-kx)/(m)`….(`1`)
`rArr F-kx=ma_(1)rArr a_(1)=(F-kx)/(m)`….(`1`)  `rArr T-kx-2F=2ma_(2)`……(`2`)
`rArr T-kx-2F=2ma_(2)`……(`2`)  `rArr3F-T=ma_(2)`.....(`3`)
`rArr3F-T=ma_(2)`.....(`3`)