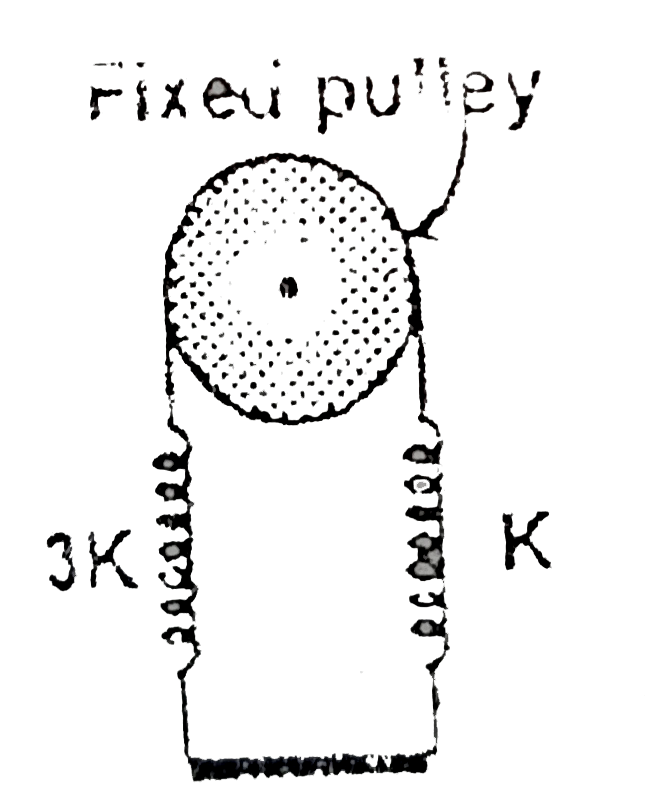A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A bar of mass m is suspended horizontally on two vertical springs of s...
Text Solution
|
- Explain the oscillations of a loaded spring and find the realtions for...
Text Solution
|
- Two bars of masses m1 and m2 connected by a non-deformed light spring ...
Text Solution
|
- A bar of mass m=0.50kg lying on a horizontal plane with a friction coe...
Text Solution
|
- Two bars of masses m(1) and m(2) , connected by light underformed hori...
Text Solution
|
- The period of oscillation of a mass M suspended from a spring of sprin...
Text Solution
|
- A spring is connected to a mass m suspended from it and its time perio...
Text Solution
|
- Find the time period of oscillation of block of mass m. Spring, and pu...
Text Solution
|
- A block of mass m is attached to a cart of mass 4m through spring of s...
Text Solution
|