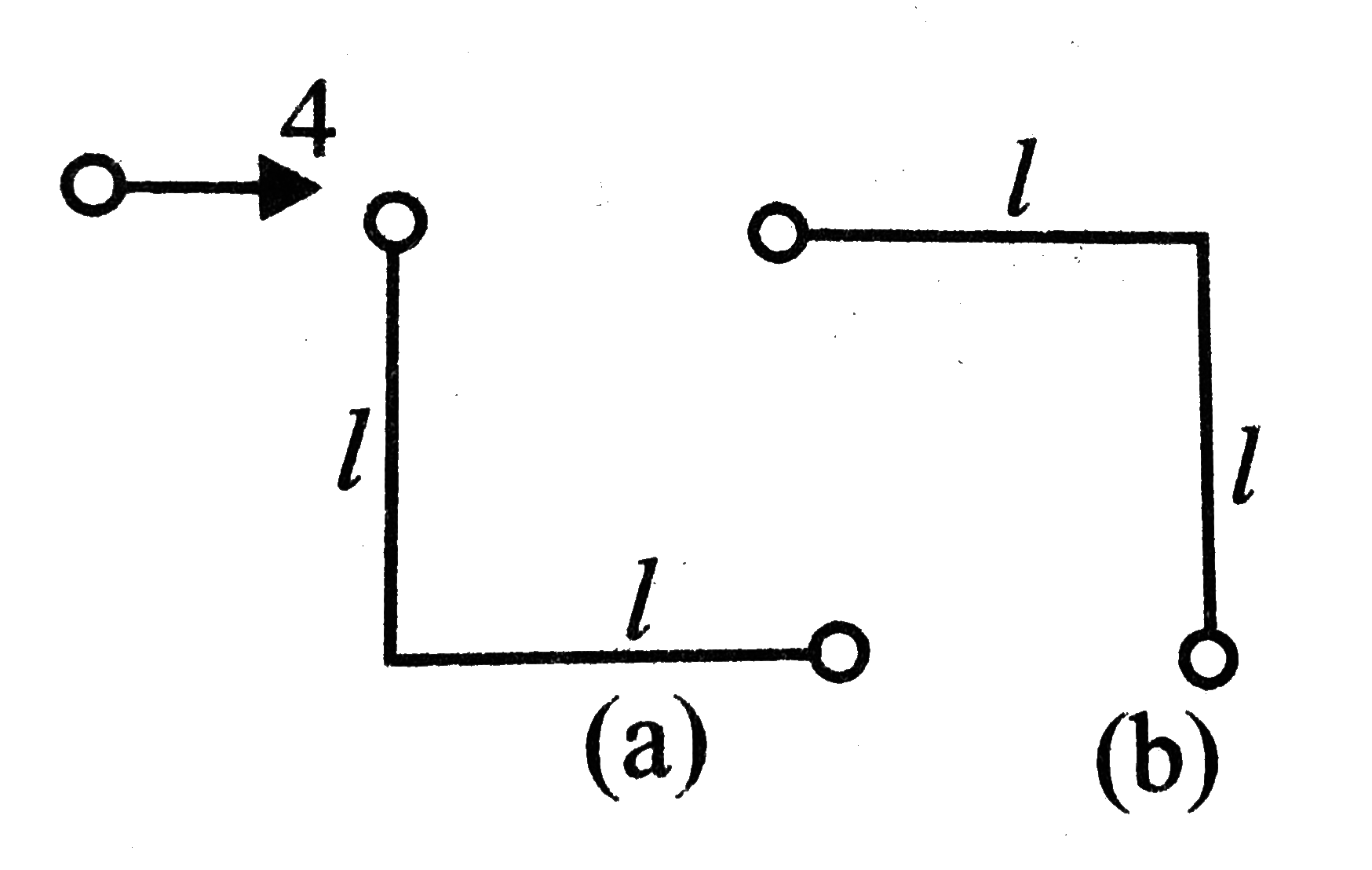
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A spherical ball of mass M moving with initial velocity u collides ela...
Text Solution
|
- A spherical ball of mass M moving with initial velocity V collides ela...
Text Solution
|
- A spherical ball of mass M moving with initial velocity V collides ela...
Text Solution
|
- A spherical ball of mass M moving with initial velocity V collides ela...
Text Solution
|
- A ball of mass M moving with a velocity v collides perfectly inelastic...
Text Solution
|
- A ball of mass m moving with a velocity v undergoes an oblique elastic...
Text Solution
|
- A billiard ball of mass M , moving with velocity v1 collides ...
Text Solution
|
- A billiard ball of mass M , moving with velocity v1 collides ...
Text Solution
|
- A ball of mass m moving with a velocity collides head on elastically w...
Text Solution
|