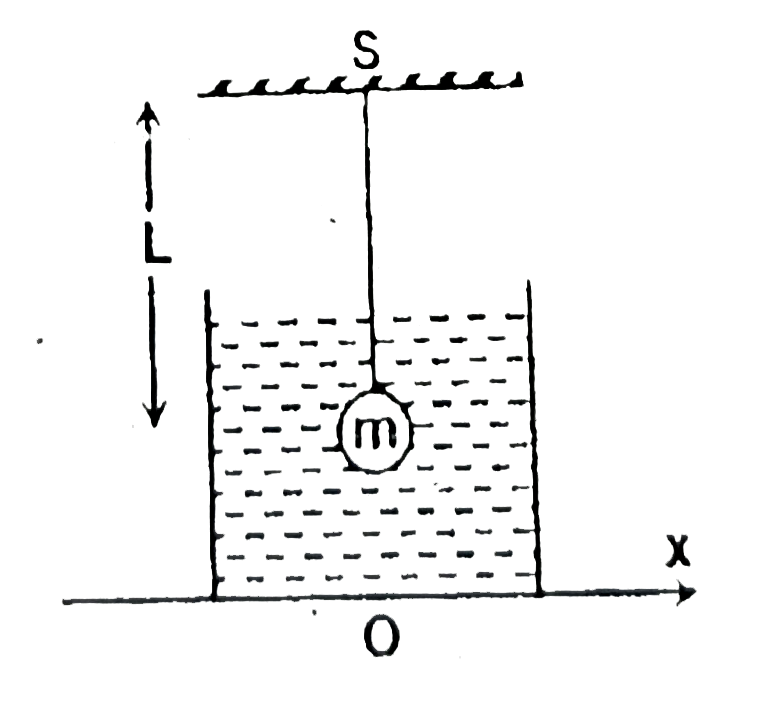
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A beaker containing an ideal fluid executes plane SHM in a horizontal ...
Text Solution
|
- A bob of mass m suspended by a light inextensible string of length 'l'...
Text Solution
|
- A small block of mass m is tied to the top of a smooth inclined plane ...
Text Solution
|
- A bob of mass 2kg is suspended from point O of a core with an inextens...
Text Solution
|
- A beaker containing an ideal fluid executes plane SHM in a horizontal ...
Text Solution
|
- A beaker containing an ideal fluid executes plane SHM in a horizontal ...
Text Solution
|
- A particle is suspended by a light vertical inelastic string of length...
Text Solution
|
- A bob of mass m attached to an inextensible string of length l is susp...
Text Solution
|
- A bob of massm attached to an inextensible string of length l is suspe...
Text Solution
|