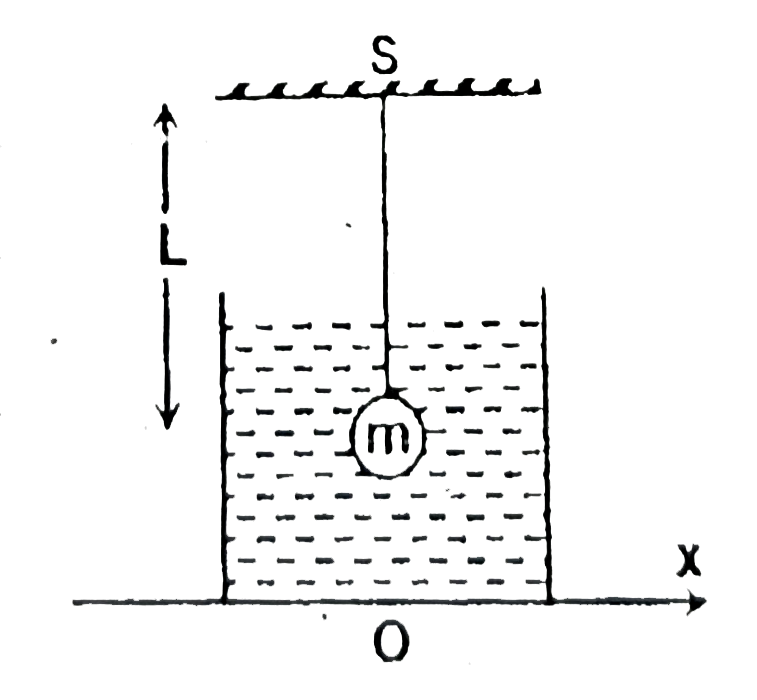
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A beaker containing an ideal fluid executes plane SHM in a horizontal ...
Text Solution
|
- The equation of a particle executing SHM is (d^(2)x)/(dt^(2))=-omega^(...
Text Solution
|
- A coical pendulum consists of a string of length L whose upper end is ...
Text Solution
|
- A bob of mass 2kg is suspended from point O of a core with an inextens...
Text Solution
|
- A uniform thin rod AB of mass M and length l attached to a string OA o...
Text Solution
|
- A uniform thin rod AB of mass M and length l attached to a string OA o...
Text Solution
|
- A beaker containing an ideal fluid executes plane SHM in a horizontal ...
Text Solution
|
- A beaker containing an ideal fluid executes plane SHM in a horizontal ...
Text Solution
|
- The shortest distance travelled by a particle executing S.H.M. from me...
Text Solution
|