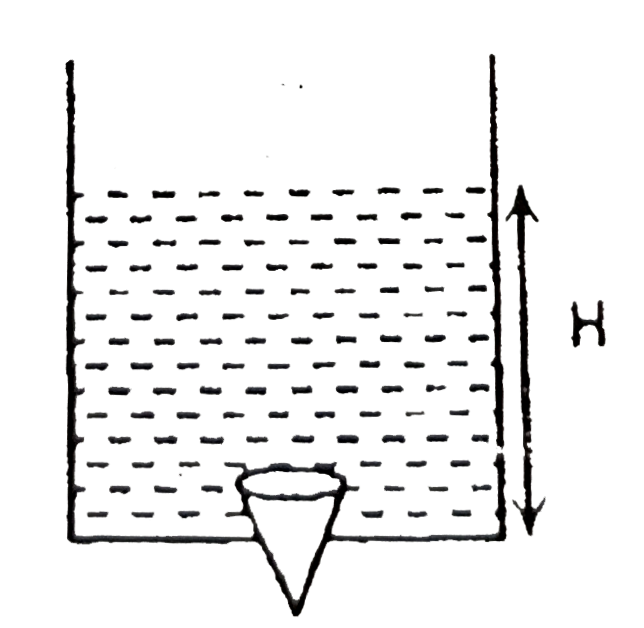
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A tank has a hole of area 2 cm^(2) at its bottom and in this hole a co...
Text Solution
|
- The level of water in a tank is 5 m high. A hole of area of cross sect...
Text Solution
|
- A tank is filled to a height H. The range of water coming out of a hol...
Text Solution
|
- एक टंकी की ऊँचाई H है। टंकी की दीवार में नीचे से h ऊँचाई पर एक सूक्ष्म...
Text Solution
|
- The level of water in a tank is 5 m high . A hole of the area 10 cm^2 ...
Text Solution
|
- A cylindrical tank is filled with water to a level of 3m. A hole is op...
Text Solution
|
- A tank of height 5m is full of water. There is a hole of cross-section...
Text Solution
|
- A large water tank has a hole in its wall near the bottom. The water l...
Text Solution
|
- A tank of height 5 m is full of water. There is a hole of cross-sectio...
Text Solution
|