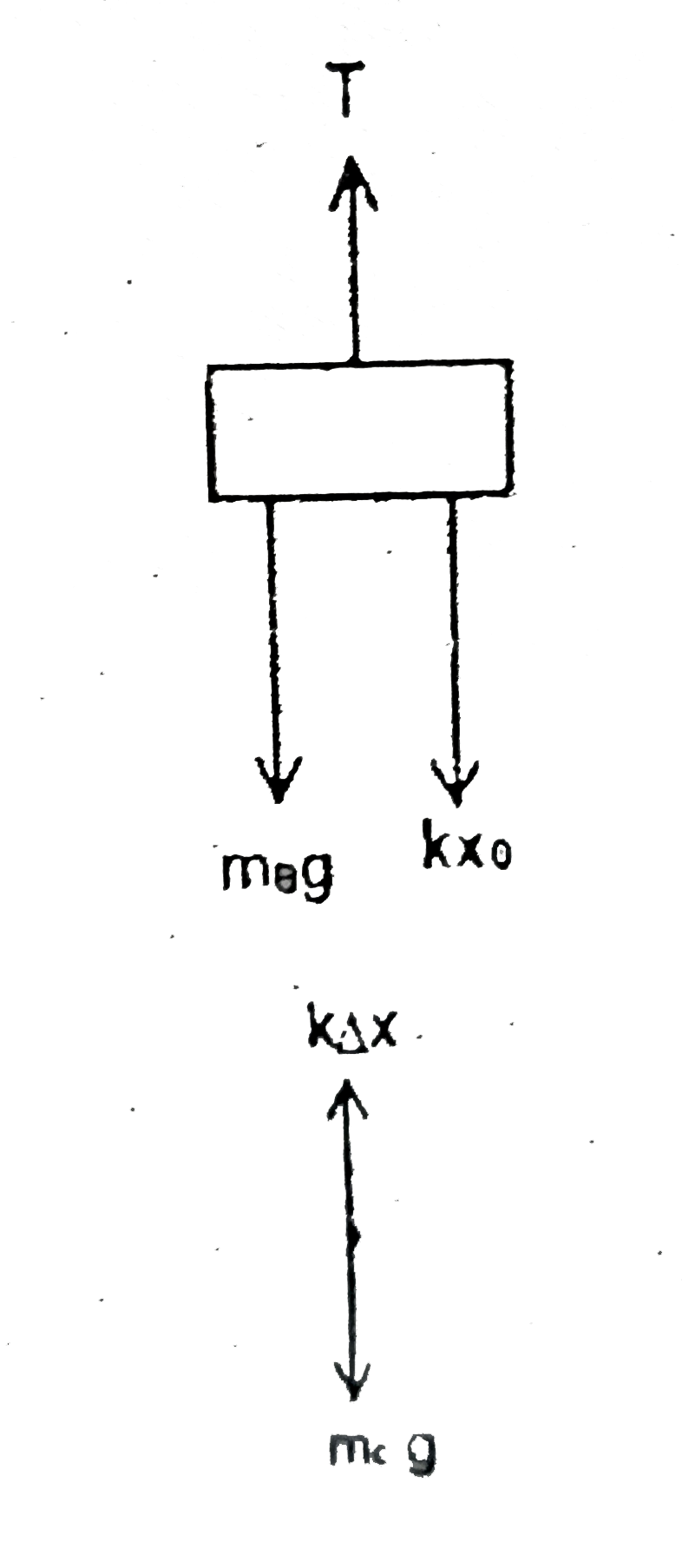
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the figure shown masses of the blocks A, B and C are 6kg, 2kg and 1...
Text Solution
|
- In the figure shown masses of the blocks A, B and C are 6kg, 2kg and 1...
Text Solution
|
- A block of mass m is connected with a rigid wall by light spring of st...
Text Solution
|
- In figure, the stiffness of the spring is k and mass of the block is m...
Text Solution
|
- A block of mass m is released from rest onto a spring. A having stiffn...
Text Solution
|
- A block with mass 0.50 kg is forced against a horizontal spring of neg...
Text Solution
|
- The coefficient of friction between the block A of mass m & block B of...
Text Solution
|
- The coefficient of friction between the block A of mass m & block B of...
Text Solution
|
- Consider the system shown in the figure. Coefficient of friction betwe...
Text Solution
|