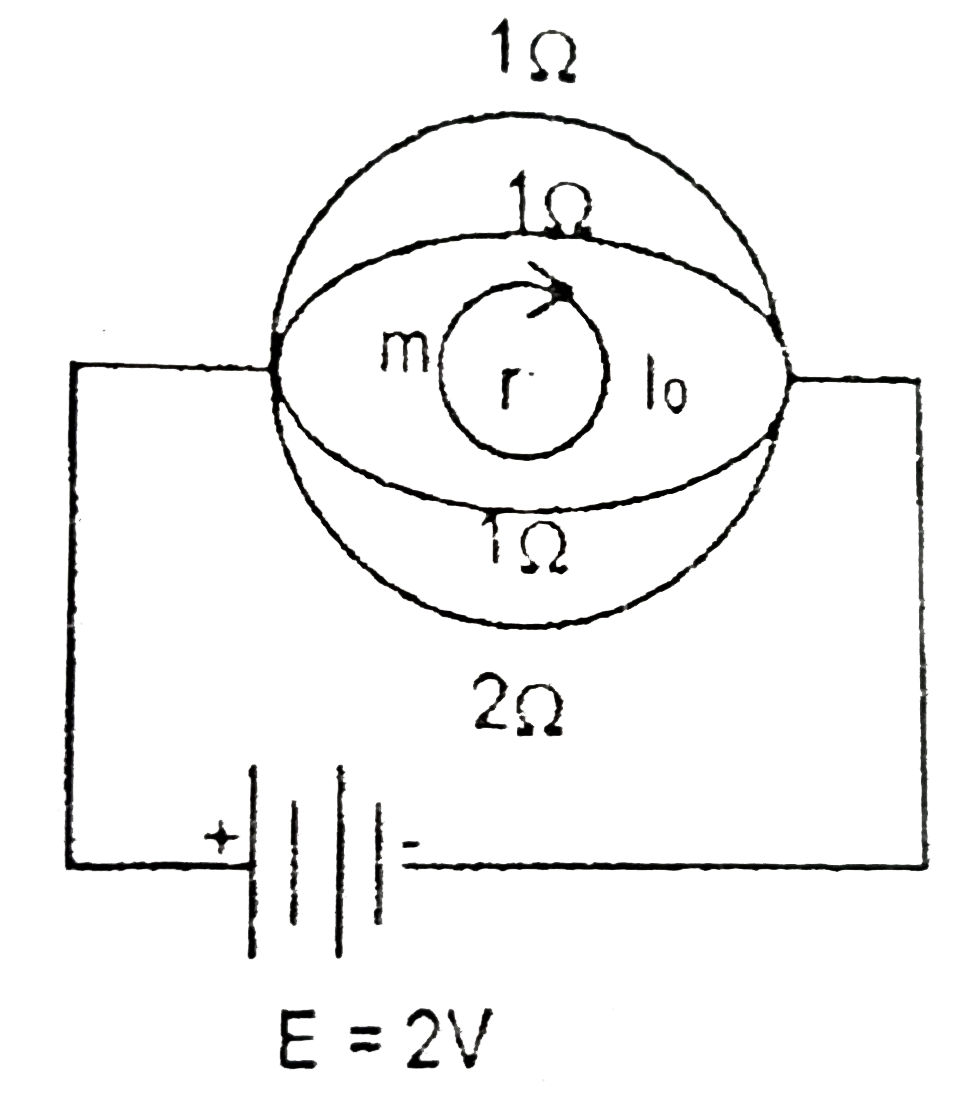
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two circular rings each of radius a are joined together such that thei...
Text Solution
|
- Two rings of same radius and mass are placed such that their centres a...
Text Solution
|
- Two circular rings each of mass M and radius R are attached to each o...
Text Solution
|
- The radius of a circular ring of wire is R and it carries a current of...
Text Solution
|
- Three rings each of mass m and radius r are so placed that they touch ...
Text Solution
|
- Two thin uniform circular rings each of radius 10 cm and mass 0.1 kg a...
Text Solution
|
- Two rings of same mass and radius R are placed with their planes perpe...
Text Solution
|
- A thin circular ring of mass M and radius R is rotating about an axis ...
Text Solution
|
- दो वलय जिनकी त्रिज्याएँ एवं द्रव्यमान समान है, एक दूसरे के साथ इस प्रक...
Text Solution
|