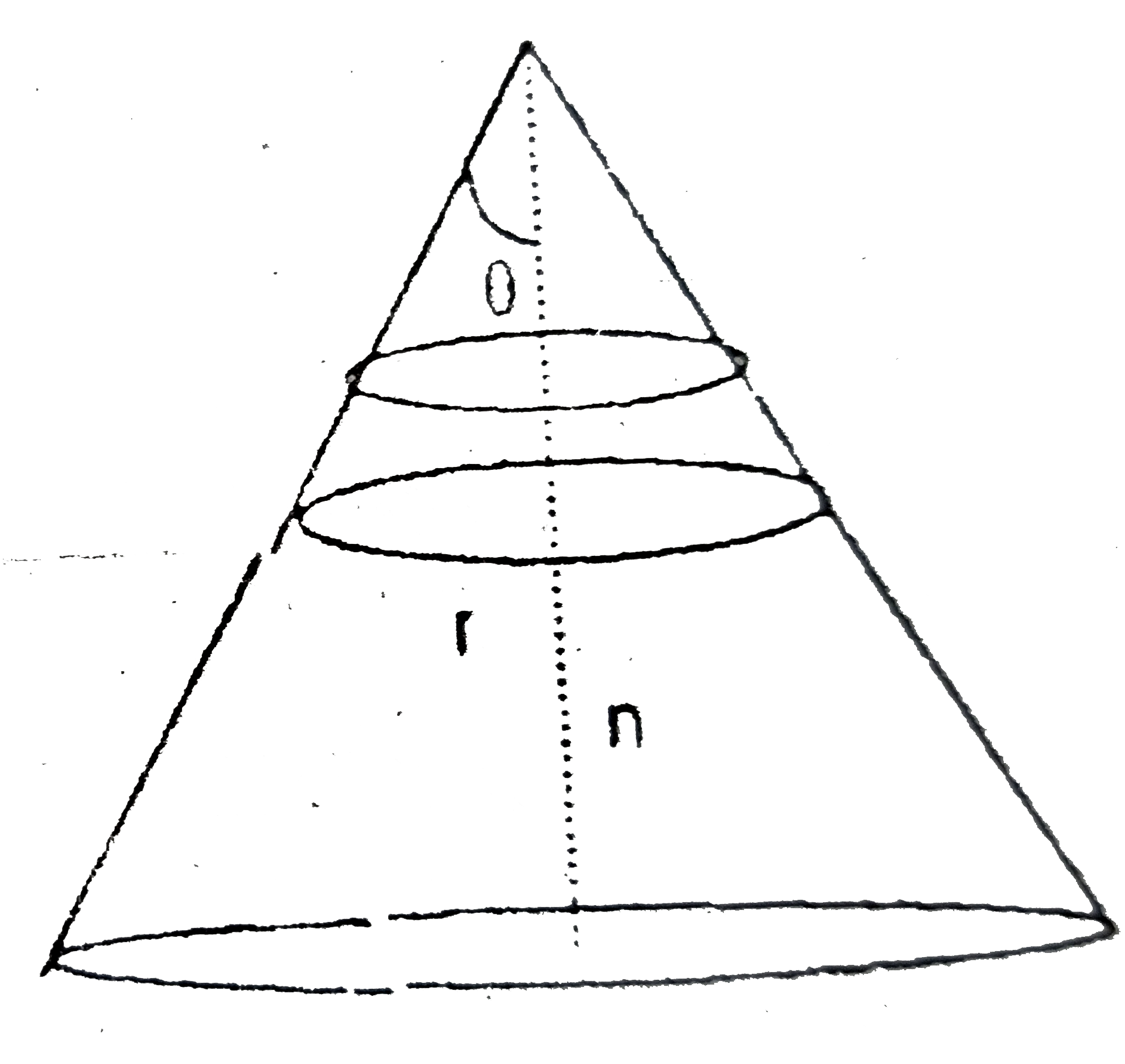
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Q charge is uniformaly distributed over the same surface of a right ci...
Text Solution
|
- A non conducting disc of radius R, charge q is rotating about an axis ...
Text Solution
|
- A hollow sphere has charge 'q' which is uniformly distributed over its...
Text Solution
|
- A flat disc of radius R charged uniformly on its surface at a surface ...
Text Solution
|
- A charge Q is spread uniformly over an insulated ring of radius R .Wha...
Text Solution
|
- A charge q is spread uniformly over an insulated loop of radius r. If ...
Text Solution
|
- A thin disc of radius R has charge Q distributed uniformly on its surf...
Text Solution
|
- A charge q is spread uniformly over an isolated ring of radius 'R'. Th...
Text Solution
|
- A charge q is spread uniformly over an isolated ring of radius ' R'. T...
Text Solution
|
 .
.