Text Solution
Verified by Experts
Recommended Questions
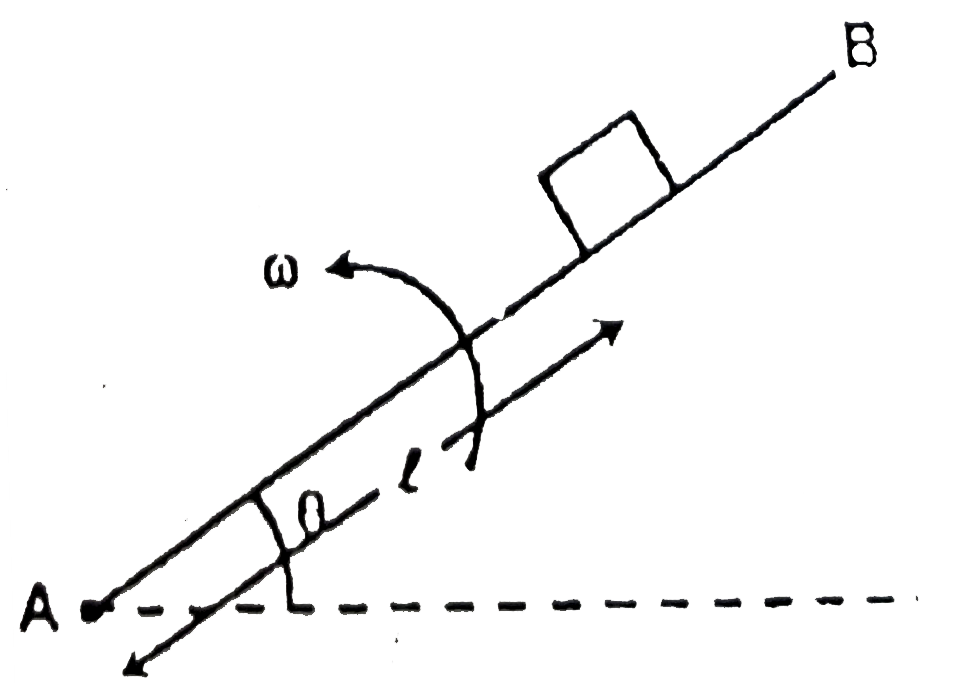
- A plank is rotating in a vertical plane about one of its ends with a c...
Text Solution
|
- A block of mass m=2kg is placed in equilibrium on a moving plank accel...
Text Solution
|
- A block of mass m=2kg is placed in equilibrium on a moving plank accel...
Text Solution
|
- A block of mass m=2kg of shown dimensions is placed on a plank of mass...
Text Solution
|
- A block is kept on a rough horizontal plank. The coefficient of fricti...
Text Solution
|
- The block of mass m is kept on plank of mass M. The block is given vel...
Text Solution
|
- A block is kept on a rough horizontal plank. The coefficient of fricti...
Text Solution
|
- A block of mass 2 kg rests on a rough horizontal plank , the coefficie...
Text Solution
|
- A plank of mass 10 kg and a block of mass 2 kg are placed on a horizon...
Text Solution
|