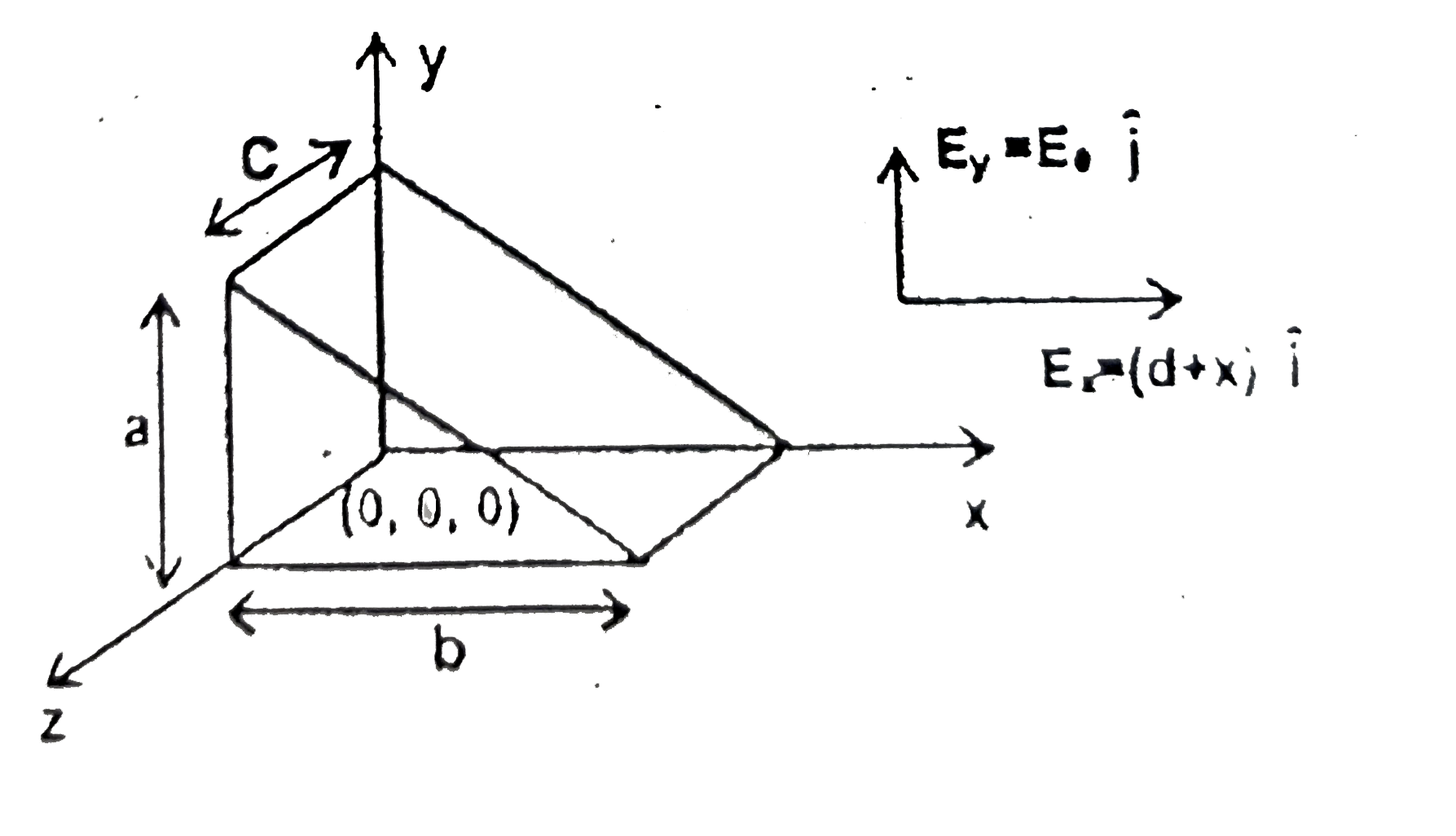
In the given electric field `vecE=[(d+x)hati+E_(0)hatj]N//Ca` hypothetical closed surface is taken as shown in figure. The total charge enclosed within the closed surface is `Kepsilon_(0)`. Then, find the value of `k`. (`a=2m`, `b=3m` and `c=2m`)

In the given electric field vecE = [alpha(d+x)hati + E_0hatj] NC^(-1) , where alpha = 1NC^(-1) hypothetical closed surface is taken as shown in figure . The total charge enclosed within the close surface is

An electric field E = (20hati + 30 hatj) N/C exists in the space. If thepotential at the origin is taken be zero, find the potential at (2 m, 2 m) .

An electric field E = (20hati + 30 hatj) N/C exists in the space. If the potential at the origin is taken be zero, find the potential at (2 m, 2 m) .

Which of the following statement is correct ? If E = 0 , at all points of a closed surface. a. the electirc flux through the surface is zero. b. the total charge enclosed by the surface is zero.

Electric field in a region is given by vec(E)=-4xhat(i)+6yhat(j) . The charge enclosed in the cube of side 1 m oriented as shown in the diagram is given by alpha in_(0) . Find the value of alpha .

The inward and outward electric flux for a closed surface unit of N-m^(2)//C are respectively 8xx10^(3) and 4xx10^(3) . Then the total charge inside the surface is [where epsilon_(0)= permittivity constant]

A closed surface encloses a net charge of -3.60 muC . What is the net electric flux through the surface? (b) The electric flux through a closed surface is found to be 780 N-m^2//C . What quantity of charge is enclosed by the surface? (c) The closed surface in part (b) is a cube with sides of length 2.50 cm. From the information given in part (b), is it possible to tell where within the cube the charge is located? Explain.

The electric field in a region is radially outward with magnitude E = 2r. The charge contained in a sphere of radius a = 2m centerd at the origin is 4x piepsi_(0) . Find the value of x.

The electric field in a cubical volume is vecE = E_0 (1+z/a) hati + E_0(z/a)hatj Each edge of the cube measures d, and one of the corners lies at the origin of the coordinates. Determine the net charge within the cube.

The electric field in a region is given by vec(E)=E_(0)x hat(i) . The charge contained inside a cubical volume bounded by the surface x=0, x=2m, y=0, y=2m, z=0 and z=2m is n epsi_(0)E_(0) . Find the va,ue of n.