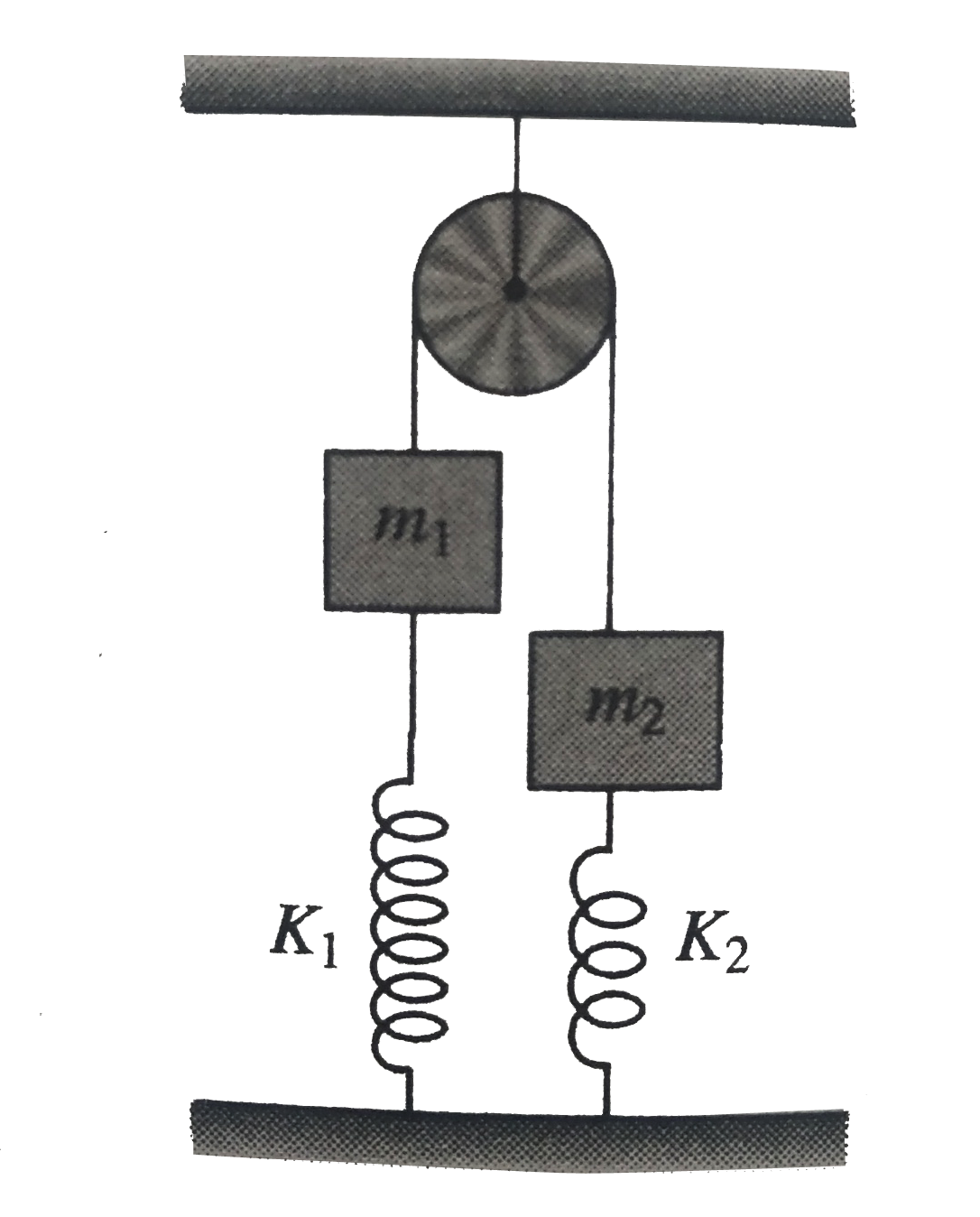
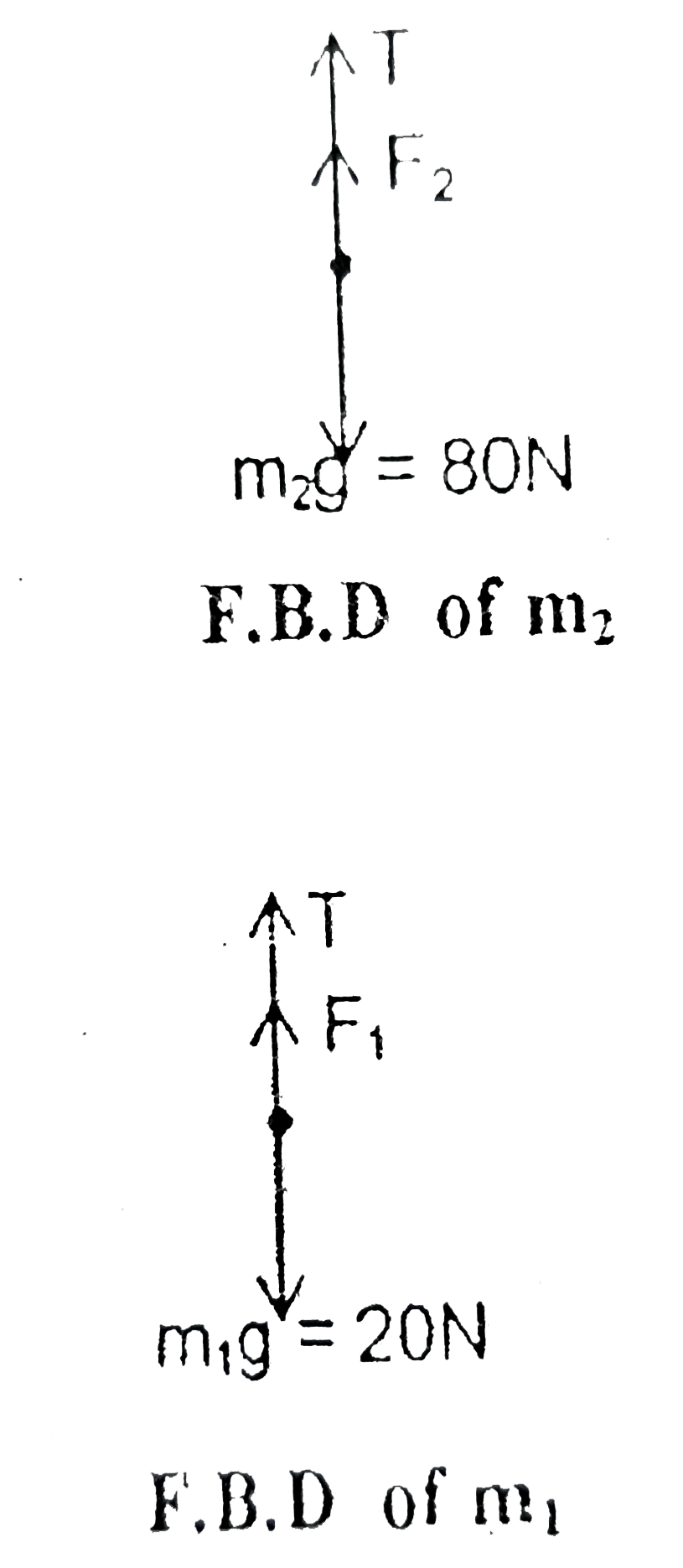A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FIITJEE-LAWS OF MOTION-Example
- A block of mass m is being pulled up a rough incline by an agent deliv...
Text Solution
|
- Find the minimum force required to keep a block of mass m in equilibri...
Text Solution
|
- Two beads of masses m(1) and m(2) are connected to each other by massl...
Text Solution
|
- Shown in the diagram is a system of two bodies, a block of mas m and a...
Text Solution
|
- Two small rings O and O' are put on two vertical stationery rods AB an...
Text Solution
|
- A fixed U-shaped smooth wire has a semi-circular bending between A and...
Text Solution
|
- Two blocks of mass 10 kg and 30 kg are kept as shown in the figure. Th...
Text Solution
|
- Two identicle particles A and B, each of mass m, are interconnected by...
Text Solution
|
- The system shown in fig is in equilibrium . Masses m(1) and m(2) are 2...
Text Solution
|
- In fig. the block of mass M is at rest on the floor . At what accelera...
Text Solution
|
- There block A B ,and C of equal mass m are placed one over the other o...
Text Solution
|
- Two blocks of masses of 0.2 kg and 0.5 kg which are placed 22m apart o...
Text Solution
|