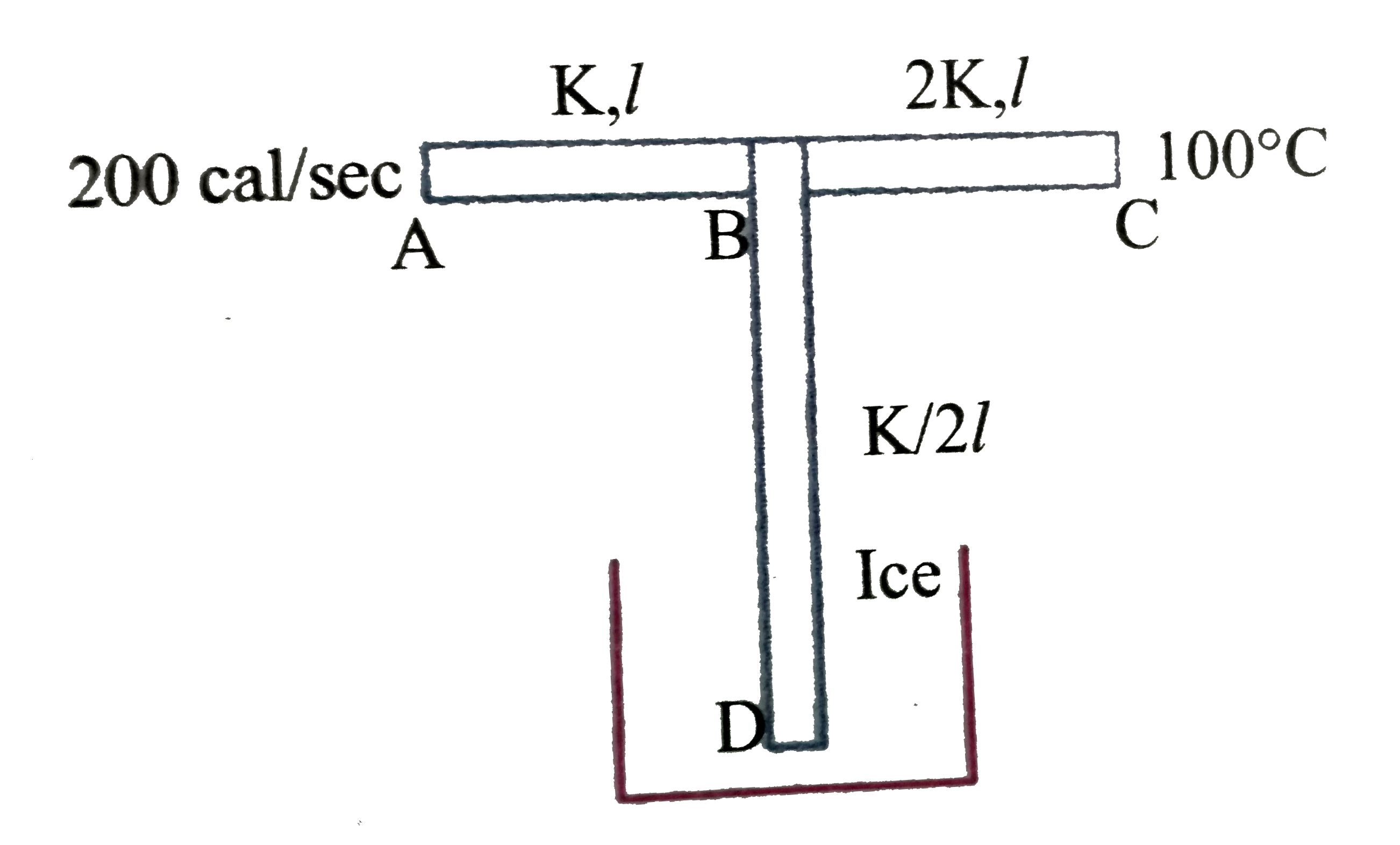
A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FIITJEE-HEAT & THERMODYNAMICS-Example
- Using the following data, find the change in temperature at which wood...
Text Solution
|
- A steel rod with a cross-sectional area of 150 mm^(2) is stretched bet...
Text Solution
|
- Air is initially at 260^(@)C and 700pa and occupied 0.028m^(3). The ai...
Text Solution
|
- A double-plane window consists of two glass sheets each of area ...
Text Solution
|
- A solid copper sphere of dimater 10mm is cooled to temperature of 150K...
Text Solution
|
- Two cylinders fitted with pistons contain equal amount of an ideal dia...
Text Solution
|
- Two identical containers A and B with frictionless pistons contain the...
Text Solution
|
- Starting with the same initial conditions, an ideal gas expands from v...
Text Solution
|
- A monatomic gas (gamma = 5/3) is suddenly compressed to (1/8) of its...
Text Solution
|
- It takes 10 minutes to cool a liquid from 61^(@)C to 59^(@)C. If room ...
Text Solution
|
- The efficiency of an ideal gas with adiabatic exponent 'gamma' for the...
Text Solution
|
- Three rods AB, BC and BD of same length l and cross-sectionsl area A ...
Text Solution
|
- A point source S of light is emitting a power P. A sphere of radius r ...
Text Solution
|
- Power radiated by a back body is P0 and the wavelength corresponding t...
Text Solution
|
 .
.