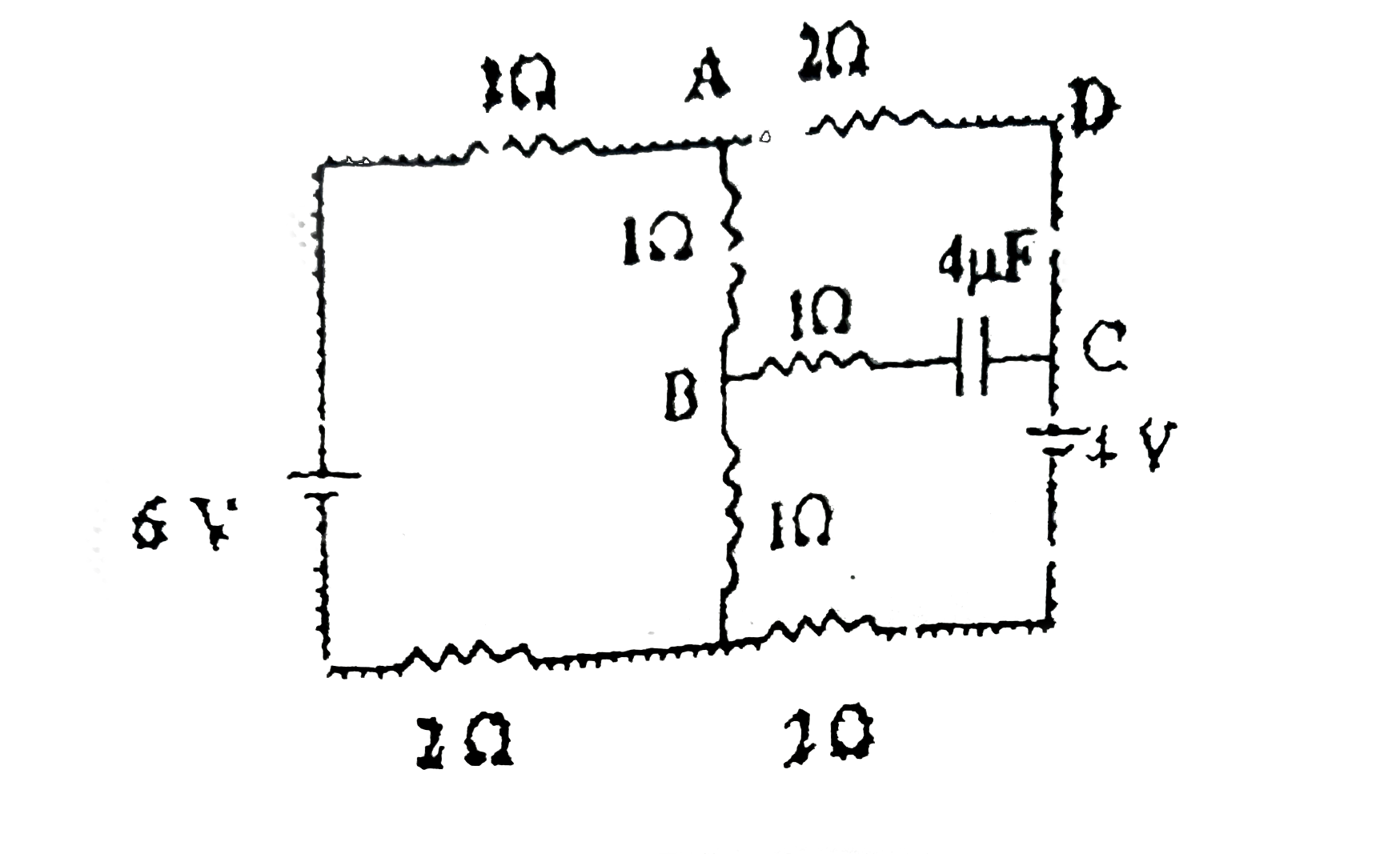
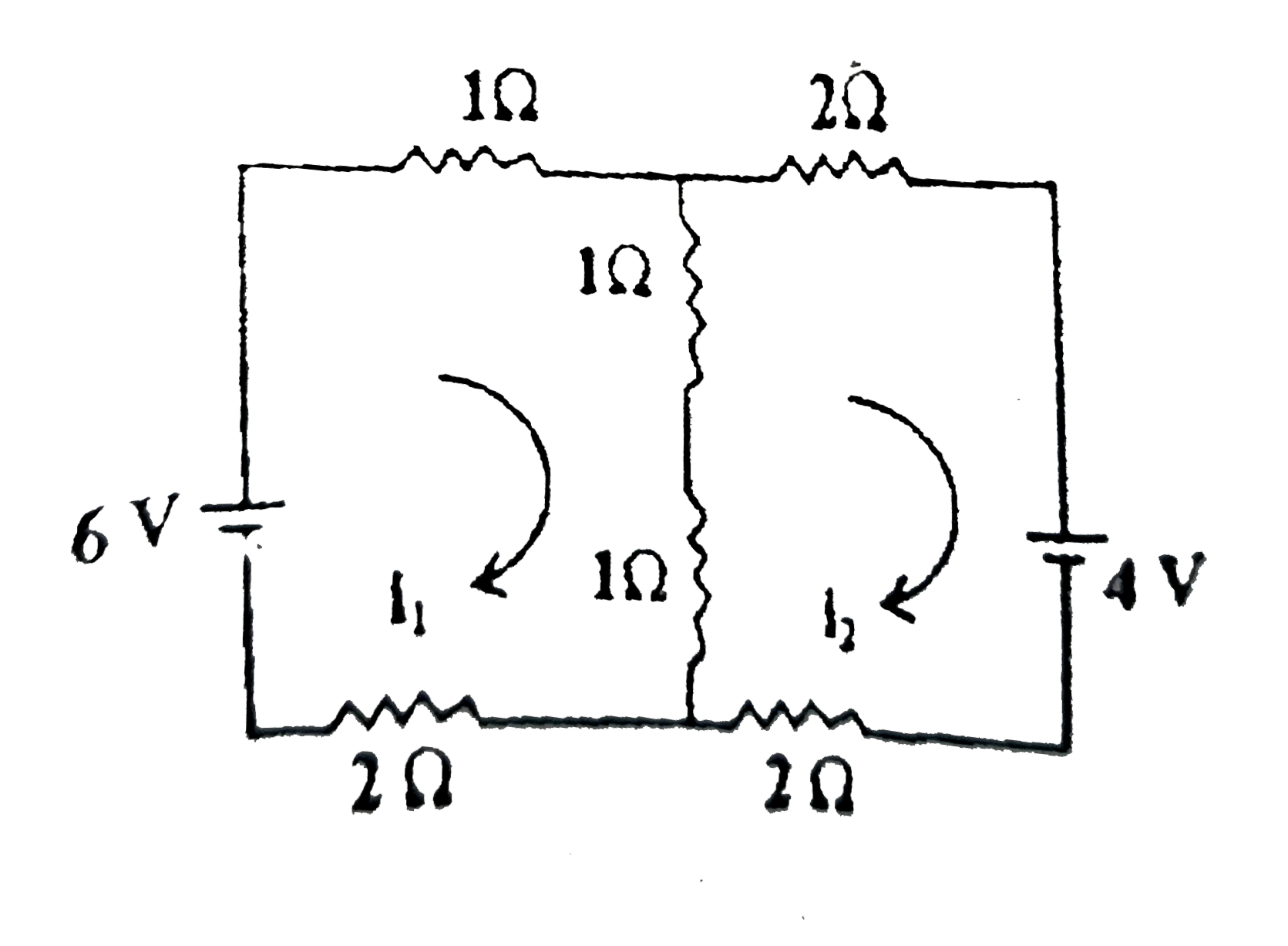
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the charge on capacitor in steady state.
Text Solution
|
- Determine the charge on capacitor in steady state:
Text Solution
|
- In the circuit shown in figure, find the steady state charges on oth t...
Text Solution
|
- For the circuit shown in the figure, find the charge stored on capacit...
Text Solution
|
- In the shown network, find the charges on capacitors of capacitances 5...
Text Solution
|
- In the circuit shown in figure find the charges on the three capacitor...
Text Solution
|
- Find the steady state charge stored in the capacitor.
Text Solution
|
- Find the steady state charge stored in the capacitor.
Text Solution
|
- In the cirucit shown in figure-3.250, find the steady state charges on...
Text Solution
|