A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
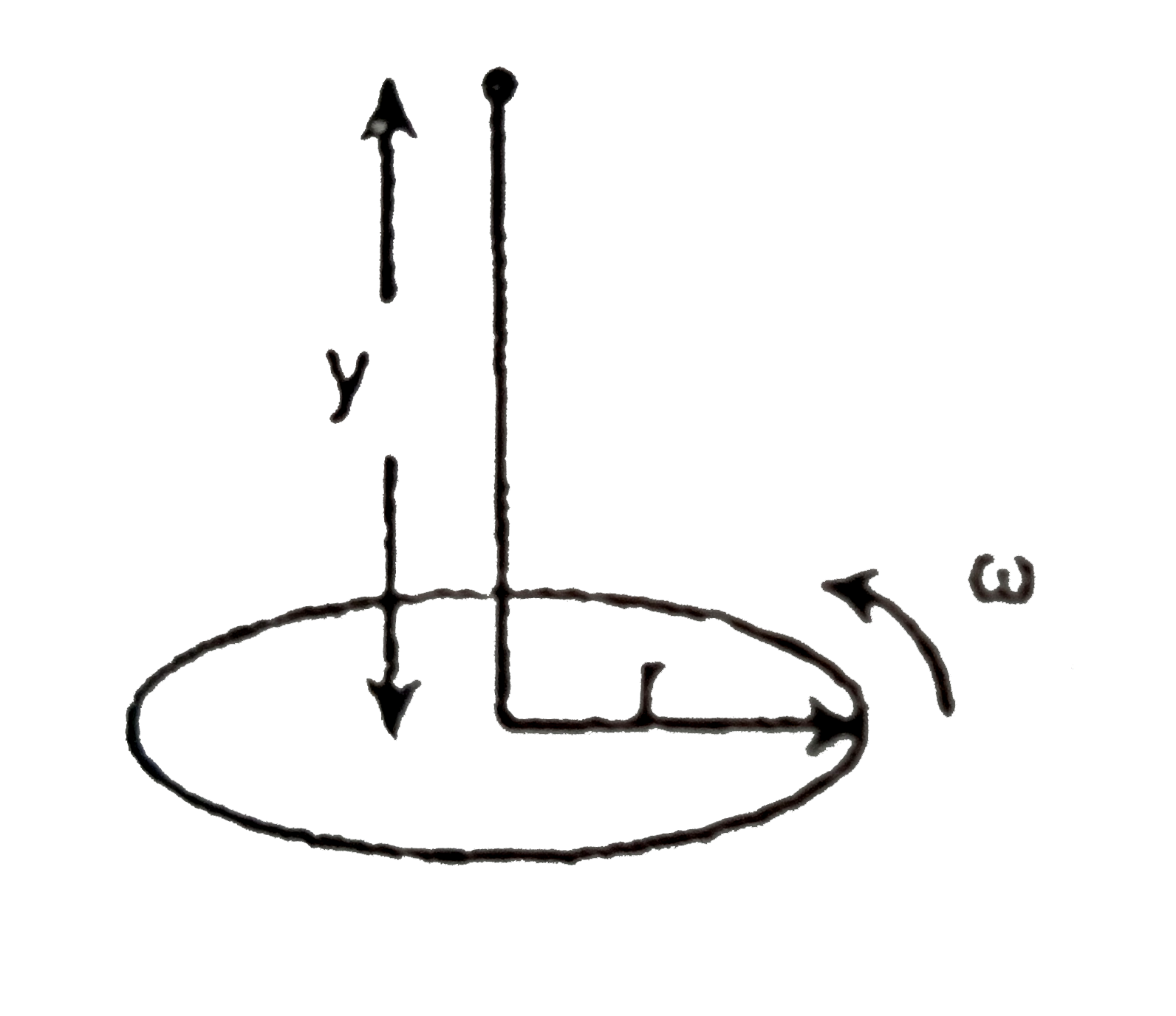
- Calculate the magnetic field at distance y from the centre of the axis...
Text Solution
|
- A flat dielectric disc of radius R carries an exces charge on its surf...
Text Solution
|
- A non-conducting thin disc of radius R charged uniformly over one side...
Text Solution
|
- A non-conducting thin disc of radius R and mass m having charge unifor...
Text Solution
|
- The surface charge density of a thin charged disc of radius R is sigma...
Text Solution
|
- A flat disc of radius R charged uniformly on its surface at a surface ...
Text Solution
|
- A disc of radius R rotates with constant angular velocity omega about ...
Text Solution
|
- A non-conducting disc having unifrom positive charge Q , is rotating a...
Text Solution
|
- Calculate electric field at a point on axis, which at a distance x fro...
Text Solution
|