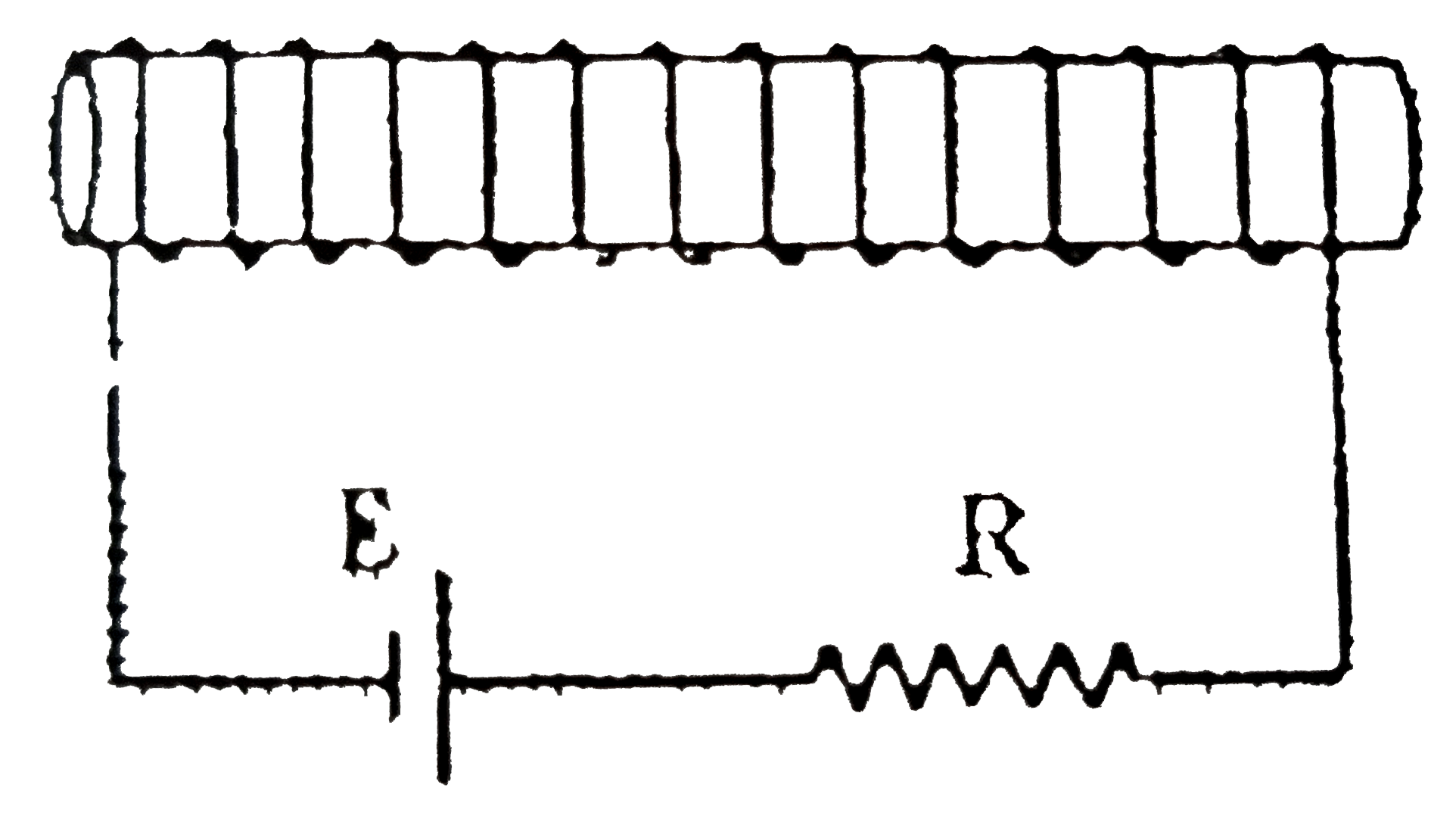
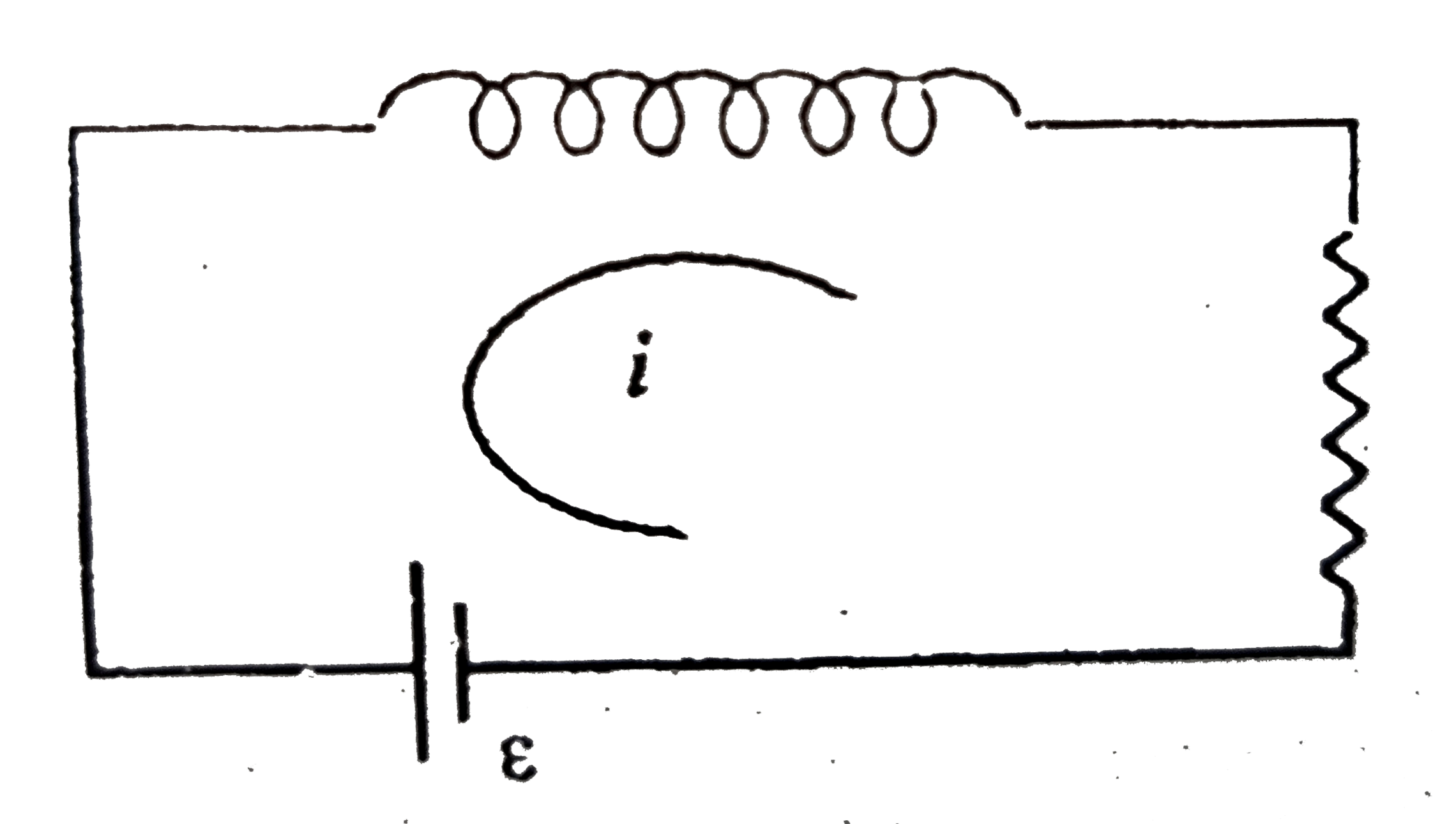
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- An iron core solenoid of length l and cross-sectional area A having N ...
Text Solution
|
- A solenoid with an iron core and a bulb are connected to a d.c. source...
Text Solution
|
- A solenoid is connected to a battery so that a steady current flows th...
Text Solution
|
- A solenoid having an iron core has its terminals connected across an i...
Text Solution
|
- A solenoid of inductance L and resistance R has a soft iron core . It ...
Text Solution
|
- A solenoid having 100 turns with an area of cross section 10 cm^(2) is...
Text Solution
|
- Steady current i flowing through a solenoid, whose core is made with a...
Text Solution
|
- A constant current is maintained in a resistive solenoid having iron r...
Text Solution
|
- परिनालिका को एक बैटरी से जोड़ा जाता है जिससे इसमें स्थायी धारा प्रवाहि...
Text Solution
|