Text Solution
Verified by Experts
Recommended Questions
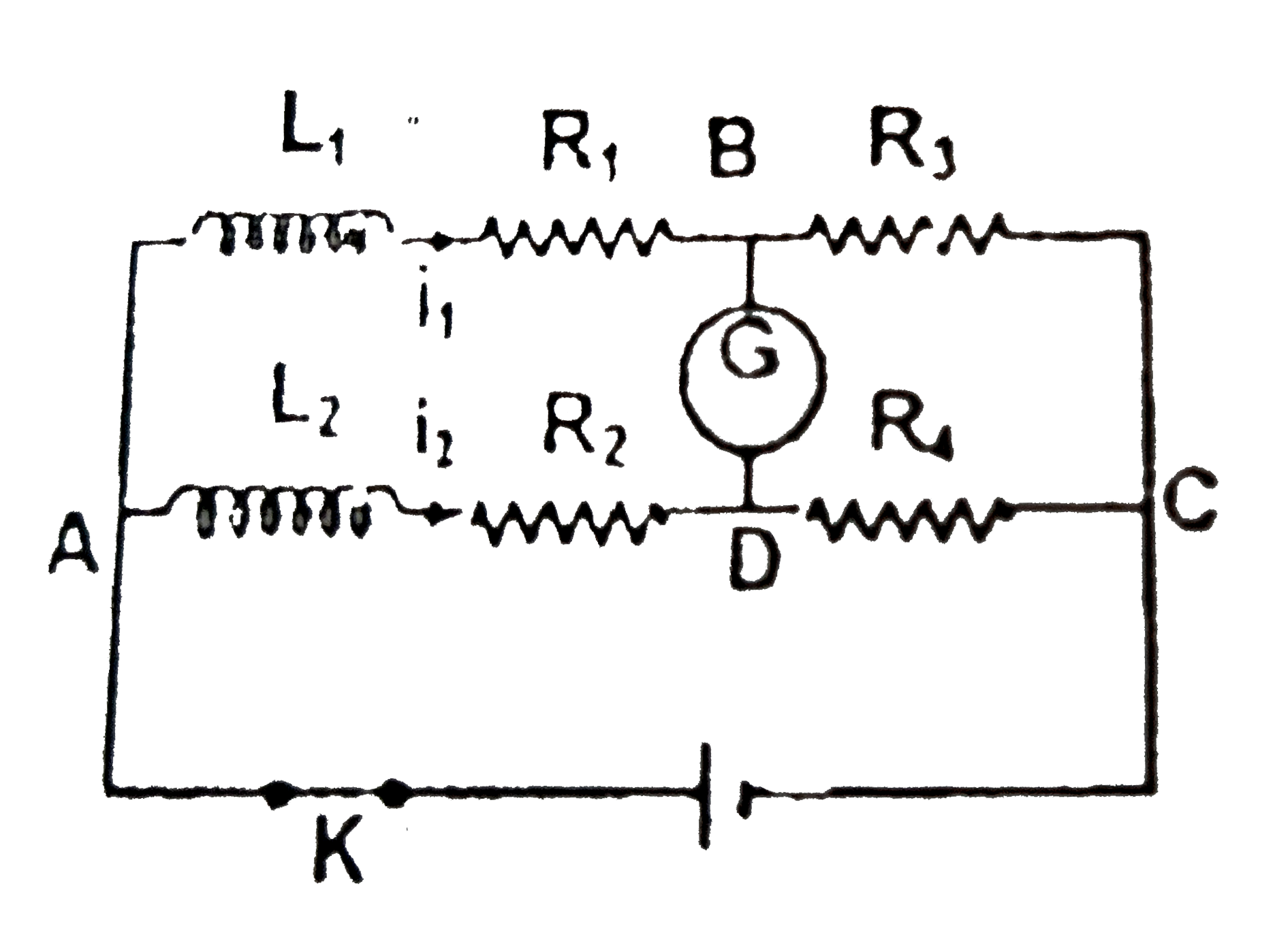
- Two inductors of self inductances L(1) and L(2) and of resistances R(1...
Text Solution
|
- In the circuit shown the key (K) is closed at t=0 , the current throug...
Text Solution
|
- A circuit contains two inductors of self-inductance L(1) and L(2) in s...
Text Solution
|
- The current growth in two L-R circuits (b) and (c) is as shown in Fig....
Text Solution
|
- In the circuit, shown in figure. R=5000Omega. If key K1 is closed, gal...
Text Solution
|
- Two coils – 1 and 2 – are mounted co axially as shown in the figure. T...
Text Solution
|
- Refer to the circuit diagram and the corresponding graphs. The current...
Text Solution
|
- If key K(1) is closed in circuit shown in figure-3.342 and galvanomete...
Text Solution
|
- Two coils of self inductance L(1) and L(2) are connected by in parllel...
Text Solution
|