Text Solution
Verified by Experts
Recommended Questions
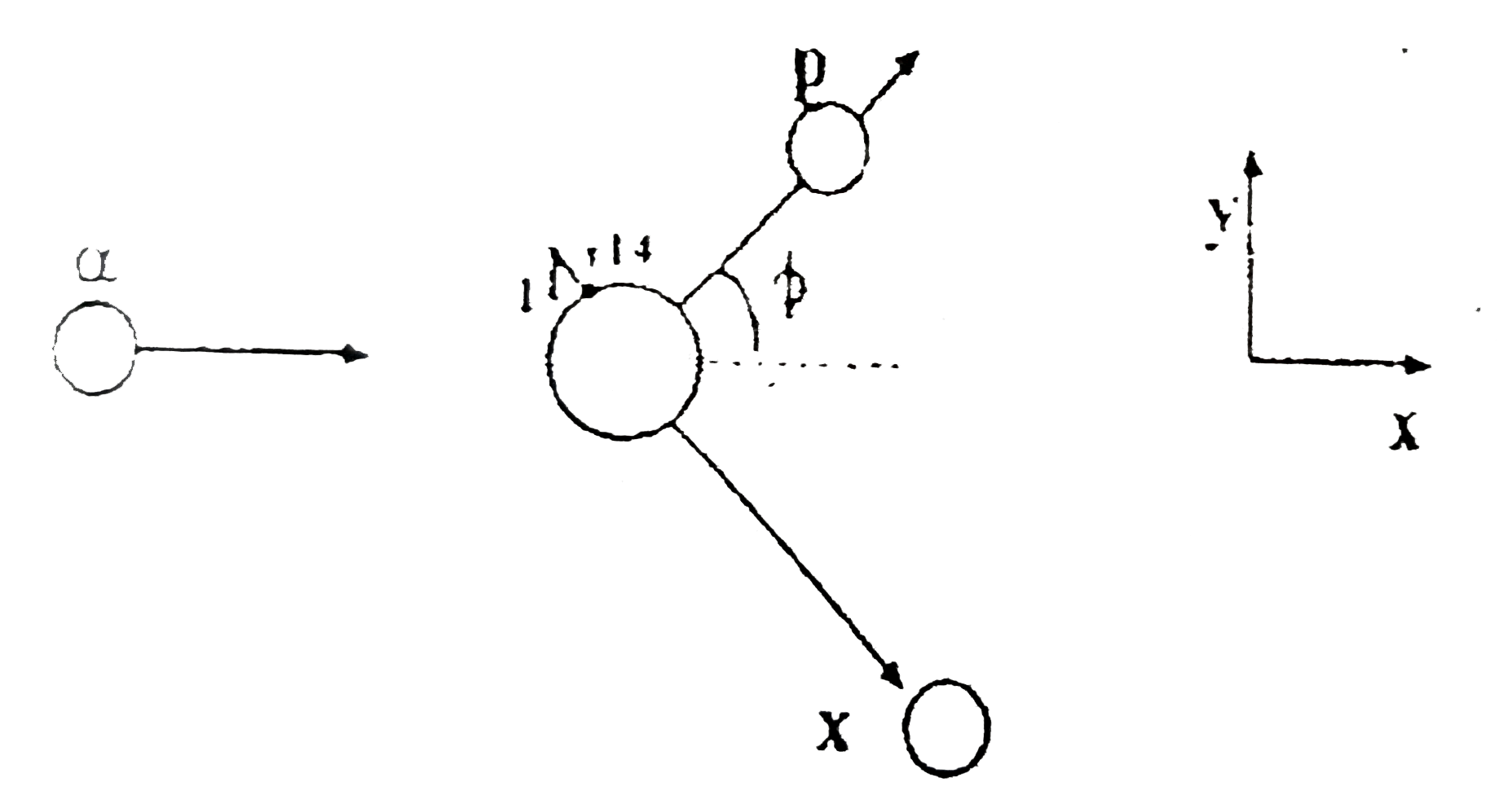
- In a nuclear reaction, alpha+"(7)N^(14)toX+p When nitrogen atoms are...
Text Solution
|
- A nucleus with mass number 220 initially at rest emits an alpha -parti...
Text Solution
|
- Find the enrgy of the reaction N^(14)(alpha,p)O^(17) if the kinetic en...
Text Solution
|
- An alpha particles kinetic energy T= 5.3 MeV initiates a nuclear react...
Text Solution
|
- Find the energy of the reaction .^(14)N(alpha, p) .^(17)O , if the kin...
Text Solution
|
- Calculate the binding energy if an alpha -particle in MeV Given : m(p)...
Text Solution
|
- यदि प्रोटॉन ,न्यूटॉन तथा alpha- कणों के द्रव्यमान क्रमशः 1.00867 amu ...
Text Solution
|
- एक प्रोटॉन तथा एक एल्फा कण किसी एकसमान चुम्बकीय क्षेत्र में क्षेत्र की...
Text Solution
|
- आरम्भ में विराम अवस्था में द्रव्यमान संख्या 220 वाला एक नाभिक , एक ऐल्...
Text Solution
|