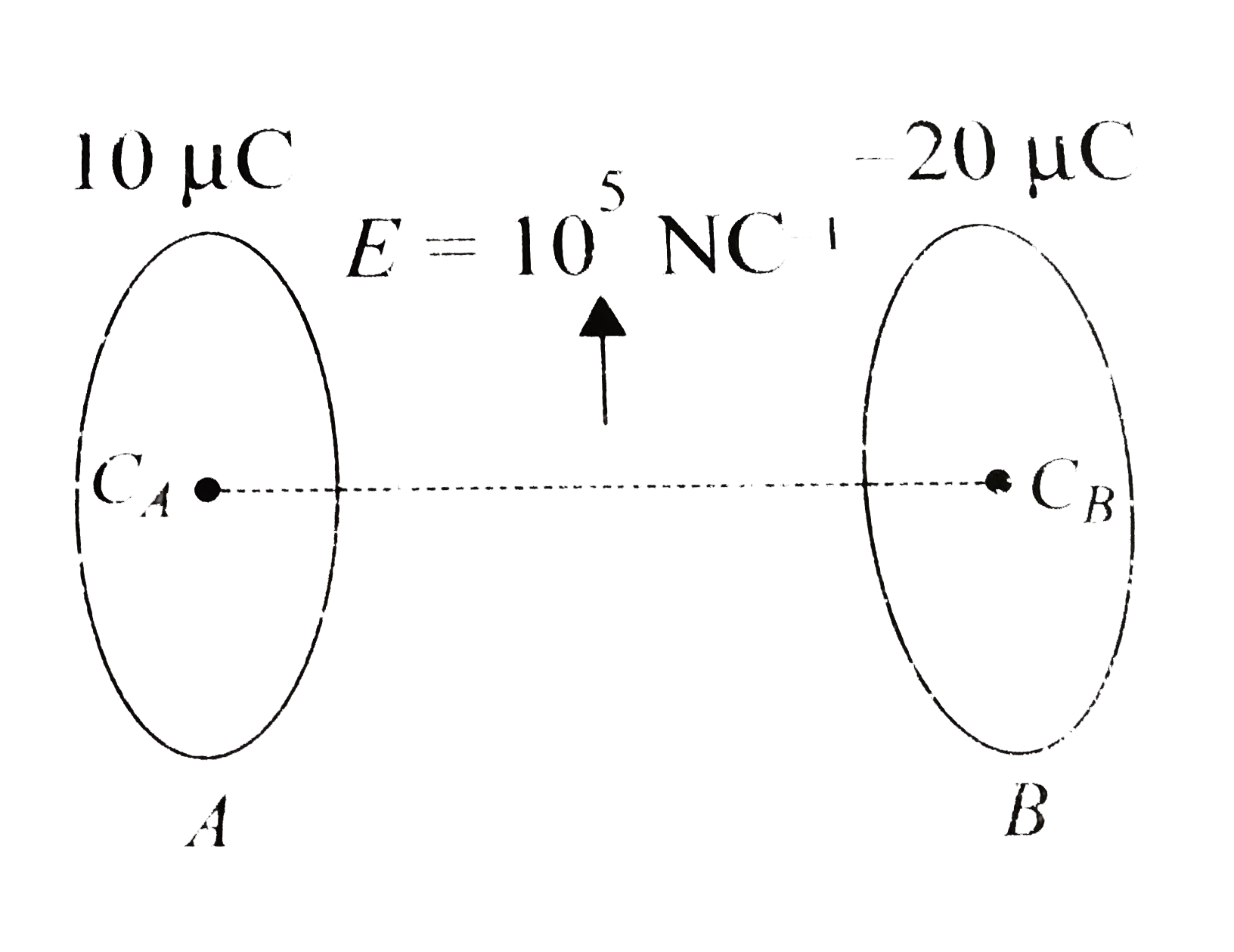Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two circular rings A and B each of radius a=30cm are placed co-axially...
Text Solution
|
- A ring of radius R has charge -Q distributed uniformly over it. Calcul...
Text Solution
|
- Two circular rings A and B each of radius a = 30 cm are placed coaxial...
Text Solution
|
- Two circular rings A and B each of radius a = 30 cm are placed coaxial...
Text Solution
|
- A ring of radius R with a uniformly distributed charge q as shown in f...
Text Solution
|
- Two identical circular rings A and B of radius 30 cm are placed coaxia...
Text Solution
|
- Two circular rings A and B, each of radius a = 30cm, are placed coaxia...
Text Solution
|
- दो समरूप पतली वलय जिनमे प्रत्येक की त्रिज्या R मीटर है, परस्पर समाक्ष ...
Text Solution
|
- A circular copper ring of radius r, placed in vacuum, has a charge q o...
Text Solution
|