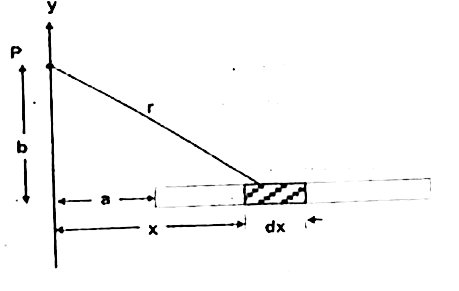
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Calculate the potential due to a thin charged rod of length L at the p...
Text Solution
|
- A rod of length l, has a uniform positive charge per unit length and a...
Text Solution
|
- A uniform rod of length L , has a mass per unit length lambda and area...
Text Solution
|
- Calculate the potential due to a thin uniformly charged rod of length ...
Text Solution
|
- Calculate the moment of inertia of a thin rod of mass m and length l a...
Text Solution
|
- Calculate the potential at a point on the perpendicular bisector of un...
Text Solution
|
- A rod length l is uniformly charged with charge q. Calculate potential...
Text Solution
|
- एक आवेश Q लम्बाई L की छड़ AB के अनुदिश एकसमान रूप से वितरित है जैसा कि ...
Text Solution
|
- Figure 22-24 shows a plastic rod having a uniformly distributed charge...
Text Solution
|