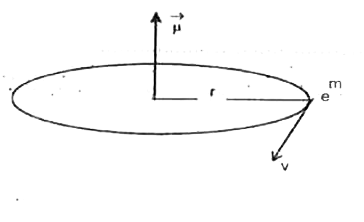
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- An electron in the ground state of hydrogen atom is revolving in antic...
Text Solution
|
- If an electron is revolving in a circular orbit of radius 0.5A^(@) wit...
Text Solution
|
- An electron in the ground state of hydrogen atom is revolving in antic...
Text Solution
|
- In a hydrogen atom, an electron carrying charge 'e' revolves in an orb...
Text Solution
|
- The orbital speed of an electron orbiting around the nucleus in a circ...
Text Solution
|
- The orbital speed of an electron orbiting around the nucleous in a cir...
Text Solution
|
- In a hydrogen atom , an electron of charge e revolves in an orbit of r...
Text Solution
|
- In a hydrogen atom , an electron of charge e revolves in an orbit of r...
Text Solution
|
- An electron in the ground state of hydrogen atom is revolving in anti-...
Text Solution
|