Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
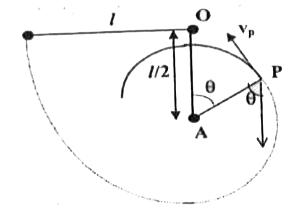
- A small ball is suspended from point O by a thread of length l. A nail...
Text Solution
|
- A small ball is suspended from point O by a thread of length l. A nail...
Text Solution
|
- A ball is suspended by a thread of length l at the point O on an incl...
Text Solution
|
- A small ball of mass m suspended from the celling at a point O by a th...
Text Solution
|
- A small ball is suspended from a point O by a light thread of length l...
Text Solution
|
- A particle of mass m and charge q is attached to a light insulating th...
Text Solution
|
- A small cork ball A of mass m is suspended by a thread of length I. An...
Text Solution
|
- Two similar balls are suspended from a point by two silk thread, each ...
Text Solution
|
- A small ball is suspended from point O by a thread of length l. A nai...
Text Solution
|