Text Solution
Verified by Experts
Recommended Questions
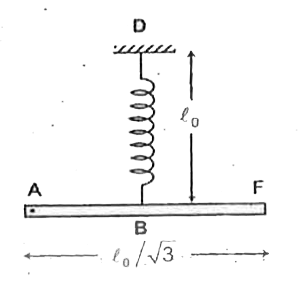
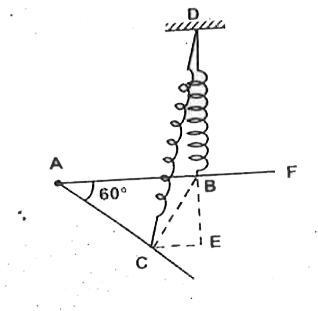
- In the figure shown one end of a light spring of natural length l(0)=s...
Text Solution
|
- A charge of 1C is placed at one end of a non conducting rod of length ...
Text Solution
|
- A thin uniform rod is free to rotate about a fixed smooth horizontal a...
Text Solution
|
- A weightless rod of length 2l carries two equal masses 'm' , one secur...
Text Solution
|
- A uniform rod AB of mass m and length L rotates about a fixed vertical...
Text Solution
|
- AB is a mass less rigid rod of length 2l. It is free to rotate in vert...
Text Solution
|
- A uniform rod of mass m and length L is fixed to an axis, making an an...
Text Solution
|
- The thin rod shown below has mases M and length L. A force F acts at o...
Text Solution
|
- A thin rod MN free to rotation in the vertical plane about the fixed e...
Text Solution
|