Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
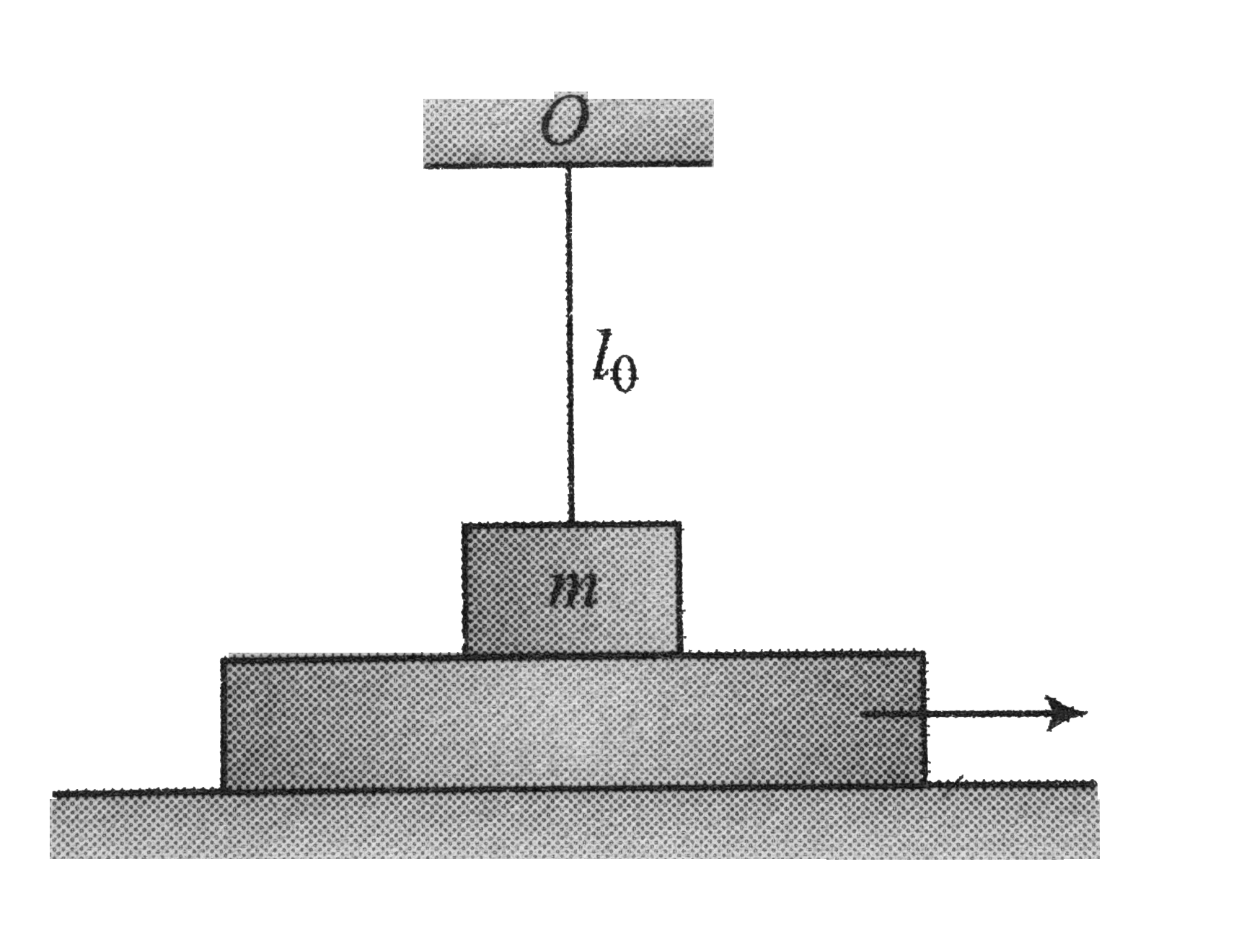
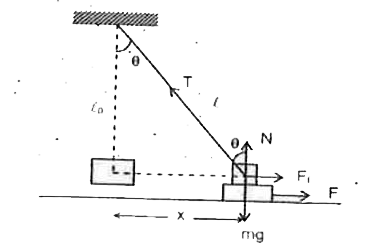
- A horizontal plane supports a plank with a bar of mass m placed on it ...
Text Solution
|
- A horizontal plane supports a plank with a bar of mass m placed on it ...
Text Solution
|
- A small bar A resting on a smooth horizontal plane is attached by thre...
Text Solution
|
- A horizontal plane supports a plank with a block placed on it. A light...
Text Solution
|
- A block of mass m=2kg of shown dimensions is placed on a plank of mass...
Text Solution
|
- A plank of mass M is placed over smooth inclined plane and sphere is a...
Text Solution
|
- A plank of mass m1 with a bar of mass m2 placed on it lies on a smooth...
Text Solution
|
- A small bar A resting on a smooth horizontal plane is attached by thre...
Text Solution
|
- A horizontal plane supports a plank with a bar of mass m=1.0kg placed ...
Text Solution
|