Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
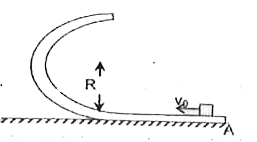
- A small block is projected with a speed v( 0) on a horizontal track pl...
Text Solution
|
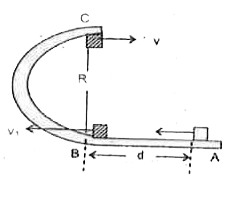
- A block weighing 10 N tavels down a smooth curved track AB joined to a...
Text Solution
|
- A small sphereical ball is released from a point at a height h on a ro...
Text Solution
|
- A section of fixed smooth circular track of radius R in vertical plane...
Text Solution
|
- A block of mass 1 kg is placed at the point A of a rough track shown i...
Text Solution
|
- A block weighing 10 kg travels down a smooth curved track AB joined to...
Text Solution
|
- A block weighing 40N travels down a smooth fixed curved track AB joine...
Text Solution
|
- A small spherical marble of mass m and radius r is rolling without sli...
Text Solution
|
- A block weighing 10 N travels down a smooth curved track AB joined to ...
Text Solution
|