Home
Class 12
PHYSICS
The potential energy function for the fo...

The potential energy function for the force between two in a diatomic molecule can approximately be expressed as `U(x)=(a)/(x^(12))-(b)/(x^(4))`, where `a` and `b` are positive constants, and `x` is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
The graph between potential energy vs `x` will be

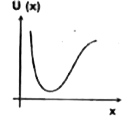
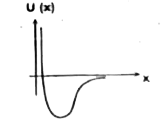
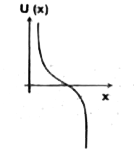
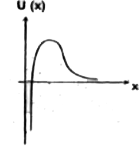
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
B
`U(x)=(a)/(x^(12))-(b)/(x^(6))`
`(delta u)/(delta x)=-(12a)/(x^(13))+(6b)/(x^(7))`
For `(delta u)/(delta x)=0 rArr (2a)/(b)=x^(6)`
For `x rArr 0 " " U rarr + oo`
For `x rarr oo " " U rarr 0` from negative side
`U=0 rArr x = root(6)(a/b)`
Hence (B) is correct.
Promotional Banner

Similar Questions

Explore conceptually related problems

The potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=(a)/(x^(12))-(b)/(x^(4)) , where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative. The graph between force between the atoms [F(x)] vs x will be

The potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=(a)/(x^(12))-(b)/(x^(4)) , where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative. The dissociation energy of the molecule is (initially molecule is at rest at equilibrium)

The potential energy function for the force between two atoms in a diatomic molecule is approximately given by U(x) =a/x^(12)-b/x^(6) where a and b are constant and x is the distance between the atoms. Find the dissoociation energy of the molecule which is given as D=[U(x- infty)-U_(at equilibrium)]

The potential energy between two atoms in a molecule is given by U(x)= (a)/(x^(12))-(b)/(x^(6)) , where a and b are positive constants and x is the distance between the atoms. The atom is in stable equilibrium when

The potential energy between two atoms in a molecule is given by U=ax^(2)-bx^(2) where a and b are positive constants and x is the distance between the atoms. The atom is in stable equilibrium when x is equal to :-

The potential energy function for a diatomic molecule is U(x) =(a)/(x^(12)) - (b)/(x^(6)) . In stable equilibrium, the distance between the particles is .

The potential energy function associated with the force vecF=4xyhati+2x^2hatj is

A particle located in one dimensional potential field has potential energy function U(x)=(a)/(x^(2))-(b)/(x^(3)) , where a and b are positive constants. The position of equilibrium corresponds to x equal to

The potential energy of a particle in a force field is: U = (A)/(r^(2)) - (B)/(r ) ,. Where A and B are positive constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is

A particle located in a one-dimensional potential field has its potential energy function as U(x)(a)/(x^4)-(b)/(x^2) , where a and b are positive constants. The position of equilibrium x corresponds to