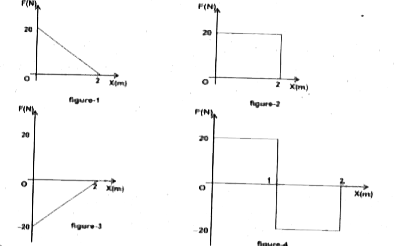
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A conservative force acts on a particle as the particle moves along ...
Text Solution
|
- The force acting on a body moving along x-axis varies with the positio...
Text Solution
|
- In the figure the variation of potential energy of a particle of mass...
Text Solution
|
- As a particle moves along the x- axis, it is acted upon by a conservat...
Text Solution
|
- A particle is to move along the x-axis from x=0 to x=x(1) while a cons...
Text Solution
|
- The force acting on a body moving along x -axis varies with the positi...
Text Solution
|
- A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...
Text Solution
|
- In the figure, the variation of potential energy of a particle of mass...
Text Solution
|
- A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...
Text Solution
|