Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
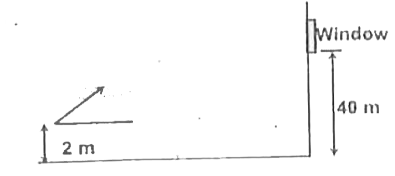
- A water jet directed by firemen must reach a window 40 m above the ...
Text Solution
|
- A 13-m long ladder reaches a window of building 12 m above the ground....
Text Solution
|
- 13m लम्बी सीढ़ी जमीन से 12m ऊँचे किसी भवन की खिड़की तक पहुँचती है भवन से...
Text Solution
|
- A folder 25 m long reaches a window of building 20 m above the ground....
Text Solution
|
- A ladder 25m long reaches a window of building 20m above the ground. ...
Text Solution
|
- A ladder 25m long reaches a window of building 20m above the ground. ...
Text Solution
|
- A ladder 25m long reaches a window of building 20m above the ground. ...
Text Solution
|
- A ladder 25m long reaches a window of building 20m above the ground. ...
Text Solution
|
- A ladder 17 m long reaches a window of a building 15 m above the groun...
Text Solution
|