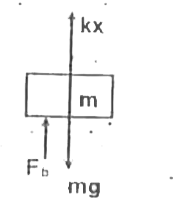
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A cube of mass m and density D is suspended from a point P by a spring...
Text Solution
|
- A rod mass (M) hinged at (O) is kept in equilibrium with a spring of s...
Text Solution
|
- A mass M is suspended as shown in fig. The system is in equilibrium. A...
Text Solution
|
- In figure, the stiffness of the spring is k and mass of the block is m...
Text Solution
|
- In figure, block A hangs by a cord form spring balance D and it submer...
Text Solution
|
- A vessel filled with water is kept on a weighing pan and the scale adj...
Text Solution
|
- A cube of mass m and densituy D is suspended from the point P by a spr...
Text Solution
|
- A disc of mass m is connected with an ideal spring of stiffness k. If ...
Text Solution
|
- A block of density 2000kg//m^3 and mass 10kg is suspended by a spring ...
Text Solution
|