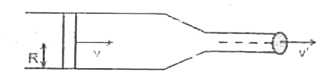
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A piston of a syringe pushes a liquid with a speed of 1 cm, / sec ...
Text Solution
|
- Figure shows a liquid being pushed out of a tube by pressing a piston....
Text Solution
|
- A spray gun is shown in the figure where a piston pushes air out of a ...
Text Solution
|
- Two syringes of different cross-section (without needle filled with wa...
Text Solution
|
- A syringe of diameter 1 cm having a nozzle of diameter 1 mm is placed ...
Text Solution
|
- An ideal liquid of density rho is filled in a horizontally fixed syrin...
Text Solution
|
- An ideal liquid of density rho is filled in a horizontally fixed syrin...
Text Solution
|
- भिन्न - भिन्न अनुप्रस्थ काट वाली दो पिचकारियों में ( बिना सुई के ) पा...
Text Solution
|
- Two syringes of different cross sections (without needles)filled with ...
Text Solution
|