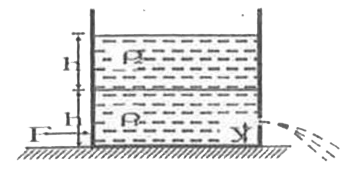
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A cylindrical tank having cross - sectional area A = 0.5 m^(2) is fil...
Text Solution
|
- A cylindrical vessel of a very large cross sectional area is containin...
Text Solution
|
- A cylindrical tank having cross-sectional area A = 0.5 m^(2) is filled...
Text Solution
|
- A cylindrical tank having cross-sectional area A = 0.5 m^(2) is filled...
Text Solution
|
- A cylindrical tank having cross-sectional area A = 0.5 m^(2) is filled...
Text Solution
|
- The level of water in a tank is 5 m high. A hole of area of cross sect...
Text Solution
|
- Two immisible liquids are pured in a U-tube having densities rho(1) = ...
Text Solution
|
- A cylindrical tank having cross - sectional area A = 0.5 m^(2) is fill...
Text Solution
|
- A cube of 1 kg is floating at the interface of two liquids of density ...
Text Solution
|