Text Solution
Verified by Experts
Recommended Questions
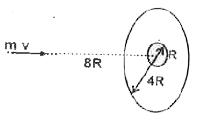
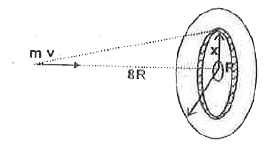
- Space junk of mass m leaves its orbit and heads towards on annular di...
Text Solution
|
- METEORS & METEORITES
Text Solution
|
- उल्का तथा उल्कापिंड में क्या अंतर है?
Text Solution
|
- उल्का और उल्कापिंड में क्या अंतर है?
Text Solution
|
- What is meteor shower?
Text Solution
|
- What is a meteor ?
Text Solution
|
- What is the other name of a meteor ?
Text Solution
|
- What is the difference between a meteor and a meteorite ?
Text Solution
|
- What is the difference between meteors and meteorites ?
Text Solution
|