Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
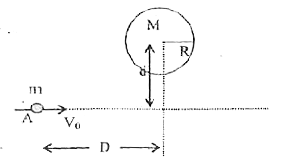
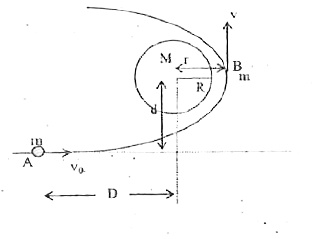
- With what speed v(0) should a body be projected as shown in the figure...
Text Solution
|
- A body is projected vertically upwards from the surface of a planet of...
Text Solution
|
- If v(e) is the escape velocity of a body from a planet of mass 'M' and...
Text Solution
|
- Gas escapes from the surface of a planet because it acquires an escape...
Text Solution
|
- Planet A has massa M and radius R. Planet B has half the mass and half...
Text Solution
|
- पृथ्वी तल पर पलायन चाल v(e) है । एक ग्रह की त्रिज्या पृथ्वी की...
Text Solution
|
- Escape velocity: V(esc) = sqrt((2GM)/(R)) for earth : V(esc) = 11....
Text Solution
|
- The escape velocity from a planet is v(0) . The escape velocity from a...
Text Solution
|
- Two planets of mass M and 16M of radius a and 2a respectively, are at ...
Text Solution
|