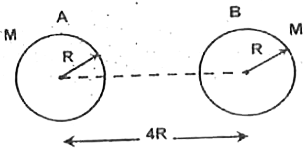
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two spherical massive bodies of uniform density each of mass M and rad...
Text Solution
|
- A particle of mass m(0) is projected from the surface of body (1) wit...
Text Solution
|
- If mass of a body is M on the earth surface, then the mass of the same...
Text Solution
|
- A fixed spherical shell of inner radius R and outer radius 2R has mass...
Text Solution
|
- Two bodies of masses m and 2m are kept at distance r apart from each o...
Text Solution
|
- A body of mass m falls from earth's surface at a height equal to twice...
Text Solution
|
- If mass of a body is M on the earth surface, then the mass of the same...
Text Solution
|
- If mass of a body is M on the surface of the earth, the mass of the sa...
Text Solution
|
- The KE required to project a body of mass .m. from the earth.s surface...
Text Solution
|